How to Calculate Internal Rate of Return in Excel

When calculating the present value of investments based on projected future contributions with varying amounts, the resulting value is compared to the initial investment required. If the present value of the investments exceeds the required investment amount, it means the return rate on the invested funds is higher than expected. But this raises the question: what is the actual rate of return on investments under these conditions?



IRR Function for Calculating the Internal Rate of Return in Excel

To calculate the internal rate of return for future investments, Excel provides the IRR (Internal Rate of Return) function. This function is closely related to the NPV function, which calculates the present value of investments. The IRR function serves to calculate the internal rate of return in Excel, where the NPV function would return a result of zero (0) for the same future contributions.

To use the IRR function, the input data must be prepared. The range of values should include at least one negative and one positive payment amount. If all amounts are positive, it would indicate that no investments are being made, only returns such as dividends or profits from sales. This is a positive scenario but unlikely in practice. Typically, investment payments occur at the beginning of a project, and income payments are made at the end. It’s not always the case, but there will always be at least one negative payment (expense) and at least one positive payment (income).

The chart below shows the timeline of dividend payments, taking into account the initial investment amount so that the IRR function returns the correct result. At the beginning of the chart is a row containing the investment amount of $300,000. The formula below displays an internal rate of return of 10.53%:

=IRR(B2:B9,8%)

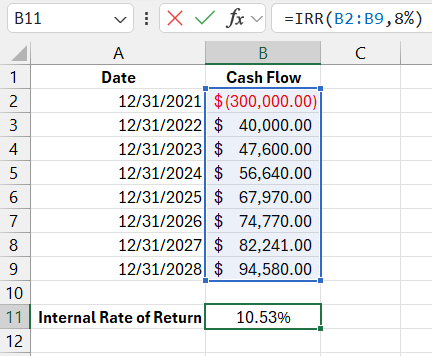
The first argument of the IRR function contains the range of cells with payments over the entire investment period:

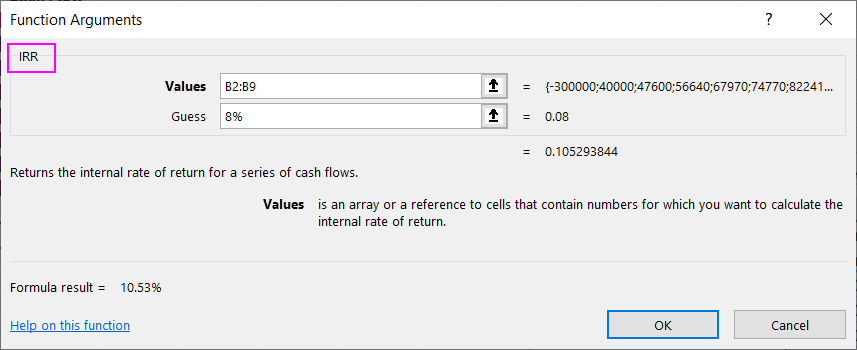
The second argument specifies the internal rate of return for the investments. If the second argument is omitted, Excel defaults to a value of 10%.

The IRR function works by calculating the present value of each payment at the given return rate. If the present value of a payment exceeds 0, the function lowers the return rate and recalculates. Excel repeats this process, adjusting the return rate and summing the present values until the total equals 0. At that point, the IRR function returns the appropriate rate of return.

Calculating the Internal Rate of Return with Irregular Payments Using XIRR

Both the IRR and NPV functions assume that all future payments are regular and made at equal intervals. However, in practice, this is not always the case. For irregular investment payments, Excel offers the XIRR function:

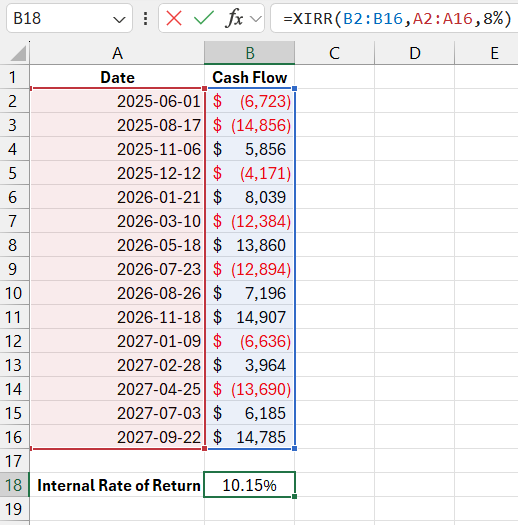
Unlike the IRR function, XIRR requires an additional argument in its syntax, which specifies the dates for each payment:

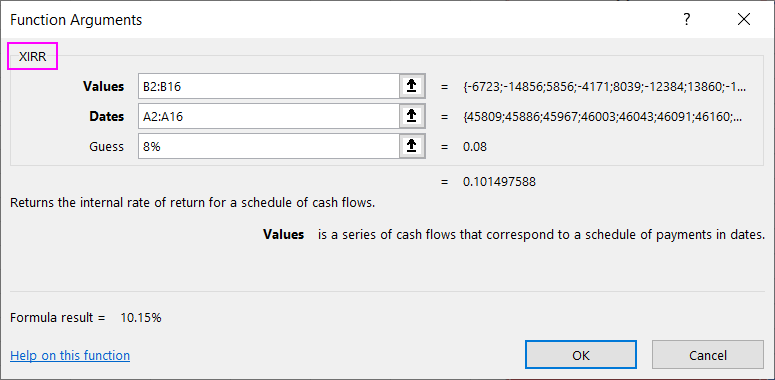
=XIRR(B2:B16,A2:A16,8%)

Download an Example of IRR Calculations in Excel

The IRR function does not require dates, as it assumes all payments are made regularly and at equal intervals. Whether the intervals are daily, monthly, or yearly doesn’t matter for the IRR function. The calculated return rate will be accurate for all specified payments. This means that for annual payments, the calculated return rate will be the annual rate. If payments are made quarterly, the result will be the quarterly internal rate of return.

Note: The XIRR function has a related function, XNPV, for calculating the present value of investments with irregular payments. This function also requires specifying the dates of the payments.

The chart below shows a timeline with irregular investment payments and dividend payouts. Sometimes investors change their strategy and make additional investments throughout the project, depending on unforeseen losses or new opportunities. Considering all the irregular payments, the investment achieves an internal rate of return of 10.14%. The XIRR function was used to calculate this rate.

The internal mechanics of the XIRR function are almost identical to the IRR function. XIRR calculates the present value of each payment individually and adjusts the internal rate of return until the result equals zero. In calculating the present value, XIRR takes into account the number of days between the date of the current payment and the previous one. The final result returned by XIRR will be the true internal rate of return for all incoming and outgoing irregular investment payments.