How to Calculate Percentages Common Formulas in Excel

You can download the examples described in this tutorial at the end of the article in the Excel file: Percentage Calculations - Common Formulas.xlsx. Writing them yourself ensures that you will remember this lesson.

Most Popular Formulas in Excel: Percentage and Margin Calculations

Often, knowledge of Excel alone is insufficient, and understanding basic mathematical formulas becomes necessary.

Many times, I have witnessed individuals with a basic economic background struggle with calculating the price excluding VAT when given the following data: the price with VAT is $100, and the VAT rate is 23%. Surprisingly, some claim they are unable to perform this calculation.

Below, I present solutions to problems that ordinary employees or job candidates frequently encounter, requiring Excel knowledge.

Formulas for Percentage Calculations in Excel

We calculate percentage increase using the following formula:

Percentage Increase = (New Value / Old Value) - 1

This formula was used in the following example to calculate a percentage increase of 25%.

The same formula can also be written in the following form:

Percentage Addition = (New Value - Old Value) / Old Value

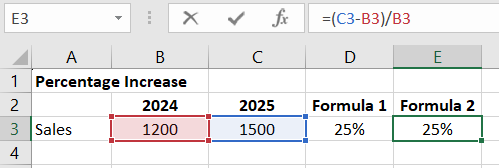
Sometimes, percentage change over a year is calculated "from the other side." In the example below, we might say that sales in 2024 were 20% less than in 2025. Those receiving this information quickly assume a difference of 20%, whereas, as calculated in example 1 (which shares the same data as the previous example), it is actually 25%.

This is a deliberate attempt to mislead the information recipient, and I do not recommend using this approach unless someone is involved in politics and must adhere to the standards accepted in that field.

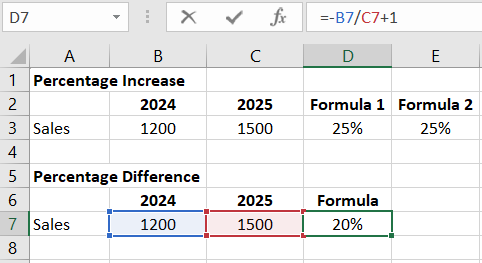
To find the percentage ratio of a specific product to the total sales volume, we divide the sales volume of that product by the total sales volume.

Percentage Ratio = Sales of Product A / Total Sales Volume

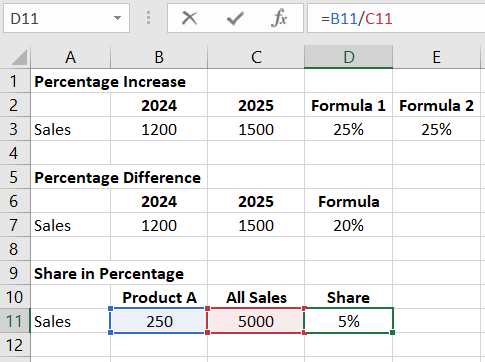
To increase a given value by a percentage, such as increasing the price by 23% for value-added tax, the following formula is used:

Price with VAT = Price without VAT * (1 + Percentage Change)

The formula for decreasing a value by a percentage looks similar, with the only difference being the use of a minus sign instead of a plus:

New Value = Old Value * (1 - Percentage Change)

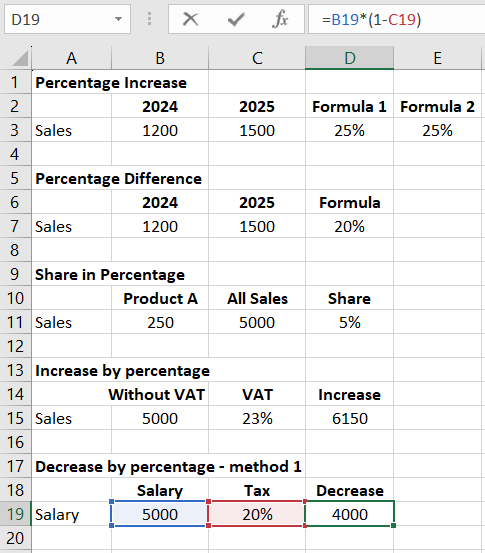
Sometimes, the percentage by which we need to decrease something is given with a minus sign (reduce by -20%), which is theoretically an error (two minuses should give a plus). Unfortunately, this variation is popular, and it should be understood as a reduction by 20%. In this case, we use the same formula as for increasing by a percentage (minus is already in %).

New Value = Old Value * (1 + Percentage Change)

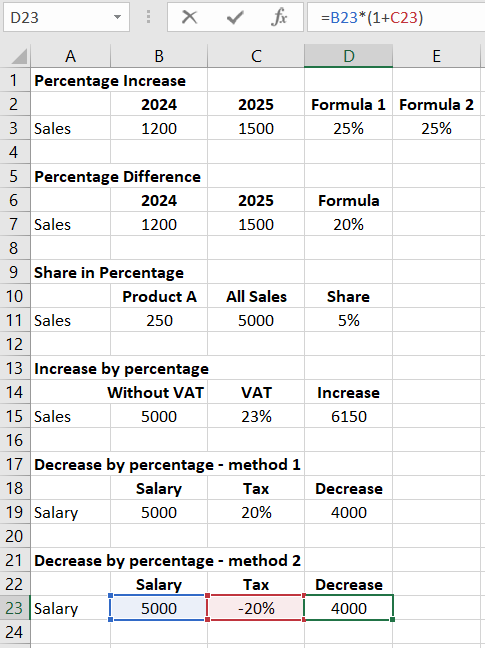
And of course, reducing a value by a percentage is one thing, while "extracting" the percentage that was added is quite another.

In the next example, we would like to find the price without VAT from the price with VAT, where VAT is 23%.

We use the following formula. To add a certain percentage to a value, we multiplied the value by (1 + %), and to "extract" the percentage, we divide the value by (1 + %) (division is the opposite operation to multiplication).

Price without VAT = Price with VAT / (1 + VAT %)

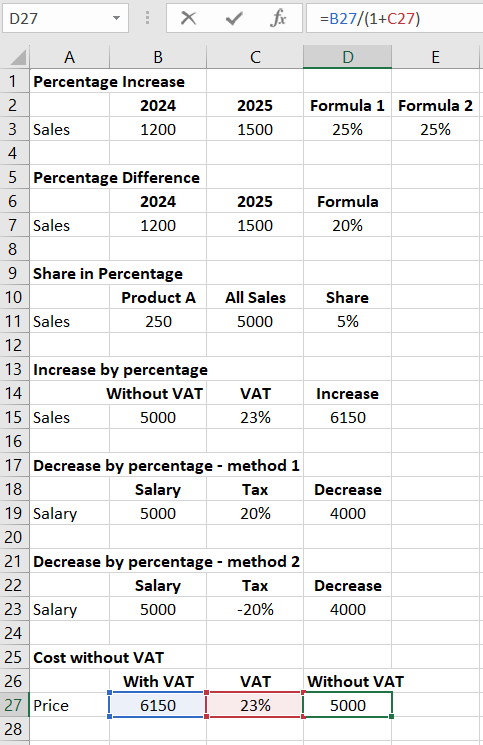
As you can see, in the example provided, we managed to obtain the initial value of the price without VAT, as shown in the two examples above.

Many people wonder why the reverse action for increasing a value by a certain percentage is not decreasing it by the same percentage.

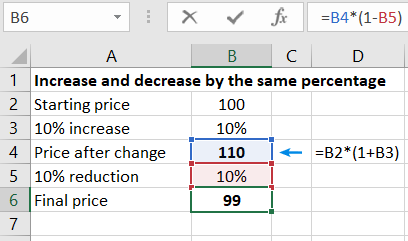
Let's consider the following example in which the price was changed twice.

The initial price was $100; it was increased by 10%, making it $110 after this change (10% of 100 is 10, 10 + 100 = 110).

After the first change, the price was decreased by 10%, resulting in $99 (10% of 110 is 11). 110 - 11 is 99).

As you can see, the price did not return to its initial value. The greater the percentage change, the greater the difference between the initial and final prices would be.

In the example below, the cost of some investment increases by 10% each year, and we want to calculate how many years it will take for this amount to double.

In the first green cell, we enter the formula for percentage increase and drag it into the following cells. We shouldn't wait ten years for this amount to double. The amount will be twice the initial sum in the seventh year, and in the eighth, it will significantly exceed its doubling. This happens because the percentage in the second and each subsequent investment year is calculated not from the initial sum, but from the already increased sum.

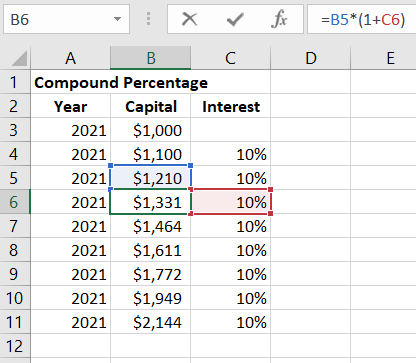
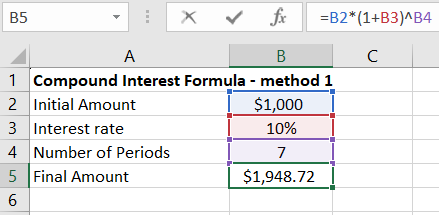
The same result can be achieved much faster using the formula for compound interest.

Final Amount = Initial Amount * (1 + Interest Rate) ^ Number of Periods

(the symbol ^ denotes exponentiation)

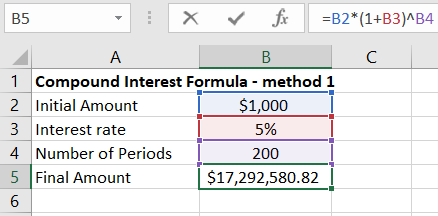
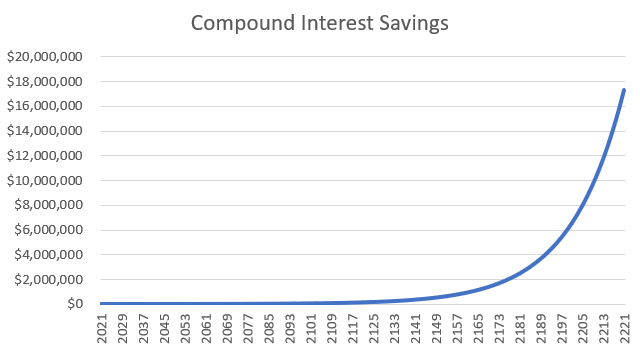
In the next example of compound interest, someone wonders if they deposited $1,000 at a fixed interest rate of 5% per annum with annual interest compounding, would their great-great-great-grandchildren be millionaires in 200 years.

Applying the above formula to such data, we get an affirmative answer to the aforementioned question. In 200 years, the account will have over $17 million.

If we decide to solve the same problem using 200 formulas for increasing by a percentage, we note that the increase in the deposit amount in the final stages is incomparably greater than in the initial periods. Over the last few years, the deposit amount increased by almost $1 million annually.

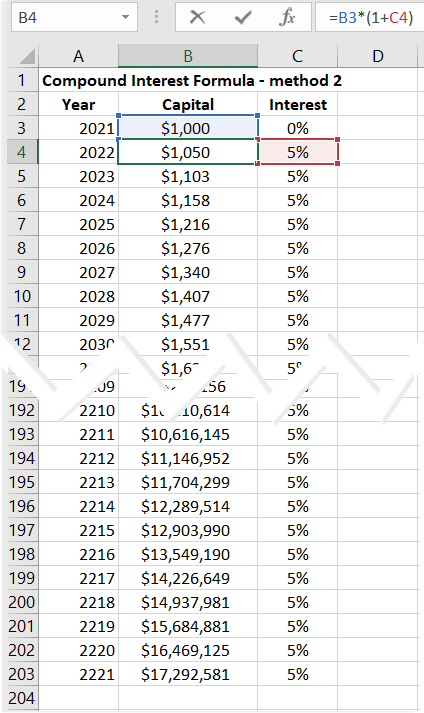
Such growth in the deposit amount in subsequent periods is typical of exponential functions, i.e., those in which the variable, in this case, the number of years, is raised to a power.

download file Download

Should we rush to banks now to open such deposit accounts? If we were to consider these calculations not as an example but seriously, we should also consider factors such as inflation, the risk of bank bankruptcy, the risk of currency devaluation of the deposit, or even a change in the system, nationalization of bank deposits, state default, or war. Taking these factors into account, a more reasonable way to invest $1,000 seems to be using them to enhance professional qualifications, such as learning Excel and VBA :-).