Presentation Julian Date Formula for Excel Visualization

Julian Dates in the (JD) format are commonly used in industries as a unified timestamp and batch identifier. This method of time encoding allows sellers, customers, and service personnel to check when a particular product was manufactured, its expiration date, and which batch it belongs to in the market. Julian Dates are also actively used in programming, the military, astronomy, and more. In this example, we will learn how to convert Julian dates to Gregorian and vice versa, creating a Julian and Gregorian date converter in Excel.



How to Convert Gregorian Date to Julian Using Excel Formula

Different industries may apply variations in Julian date formats, but the most common format consists of two parts:

1. Two-digit numeric year value.
2. Ordinal number of the day in the same year.

For example, the date 1960-01-01 corresponds to the Julian date 601, and the date 2014-12-31 corresponds to the Julian date 14365. Note that this format is not based on the Julian calendar.

Excel does not have built-in functions to convert Gregorian dates to Julian. However, the solution shown in the image below implements a formula that provides the required date format:

As seen in the image, this formula consists of two parts joined by the ampersand (&) symbol:

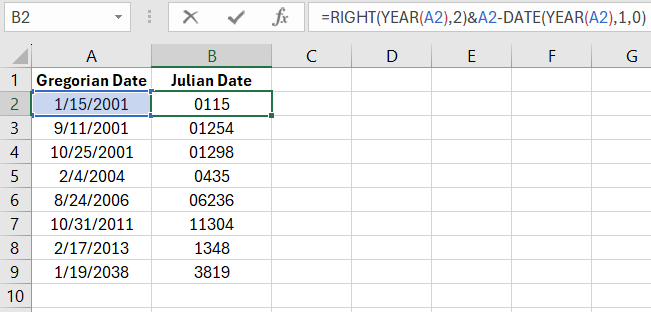
=RIGHT(YEAR(A2),2)&A2-DATE(YEAR(A2),1,0)

1. The first part uses the RIGHT text function. It extracts the last 2 digits of the year. Note that the text to extract is the result of the YEAR function, which separates the year value from the date.

=RIGHT(YEAR(A2), 2)

2. The second part of the formula is more complex. It calculates the number of days that have passed since the beginning of the year in the given date. For this, it subtracts the date of the last day of the previous year from the specified date.

A2 - DATE(YEAR(A2), 1, 0)

Note that the DATE function is used in the formula, allowing the generation of a date from three arguments: year, month, and day.

The year can be any number in the range of 1900 to 999999. The month and day can be any numbers, both positive and negative.

For example, the formula below returns the serial number for December 1, 2014:

=DATE(2014, 12, 1)

In the formula used in this example, which returns the Julian date in the third argument of the DATE function where days should be specified, the number 0 is used. This means that Excel should determine the day before the first day of the first month. For example, the formula below in an empty cell will display the date December 31, 1959:

=DATE(1960, 1, 0)

The values returned by the two formulas described above, combined using the ampersand operator "&," allow converting the standard date to the Julian date, consisting only of two numbers: the year and the ordinal number of the day from the beginning of the same year.

Alternative Formulas for Converting Dates to Julian Format in Excel

Let's create an alternative formula for converting dates to the Julian JD format:

=RIGHT(YEAR(A2),2)&DATEDIF(DATE(YEAR(A2),1,0),A2,"YD")

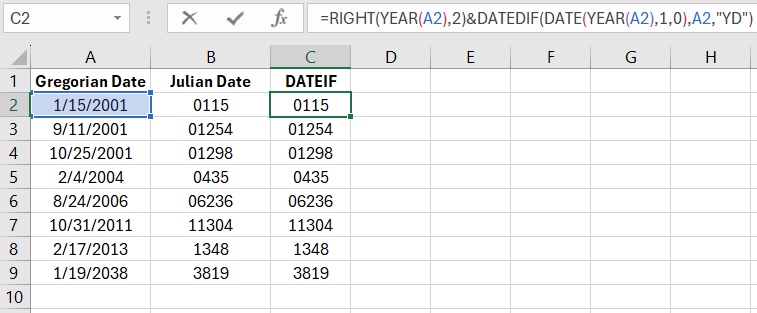
As seen in the image, we simply replaced the second part of the formula with the DATEDIF function, specifying the code "YD" in the third argument. Thanks to this, the function returns the ordinal number of the day in the incomplete year of the source date without considering full years.

An even simpler way is to use the TEXT function:

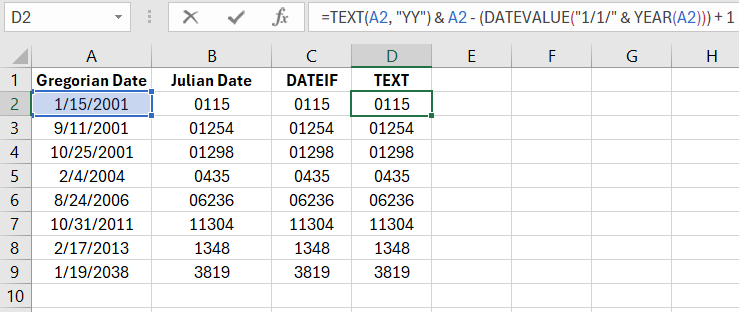
This is the shortest formula, but with a slight trick. It relies on Excel's habit of interpreting and converting certain text and numbers into dates. It would be advisable to add the DATEVALUE function to convert the text representation to a date. Therefore, a more correct version of the formula will be slightly longer and look like this:

=TEXT(A2, "YY") & A2 - (DATEVALUE("1/1/" & YEAR(A2))) + 1

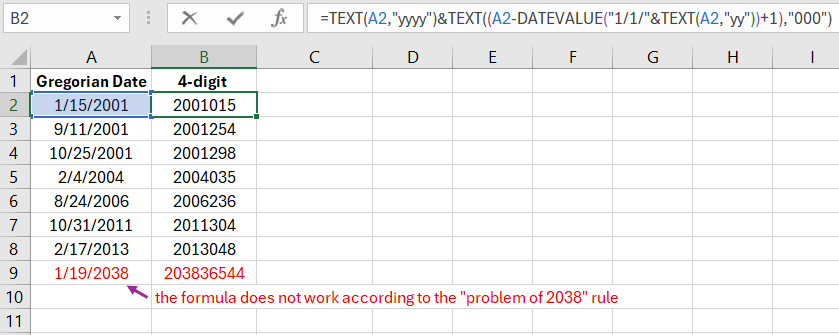
Conversion in the Format of a 4-Digit Year and a 3-Digit Day

An example of how to convert a Gregorian date to a Julian date in the format of a 4-digit year and a 3-digit day in Excel. The following formula:

=TEXT(A2,"yyyy")&TEXT((A2-DATEVALUE("1/1/"&TEXT(A2,"yy"))+1),"000")

In Excel, there are always several ways to solve a particular task. This versatile analytical and computational software tool always provides its users with freedom of choice.

Reverse Conversion of Julian Date to Gregorian

To convert the same values in the reverse direction, we will use the following formula:

=DATEVALUE("01/01/20"&LEFT(D2,2))+MID(D2,3,LEN(D2))-1

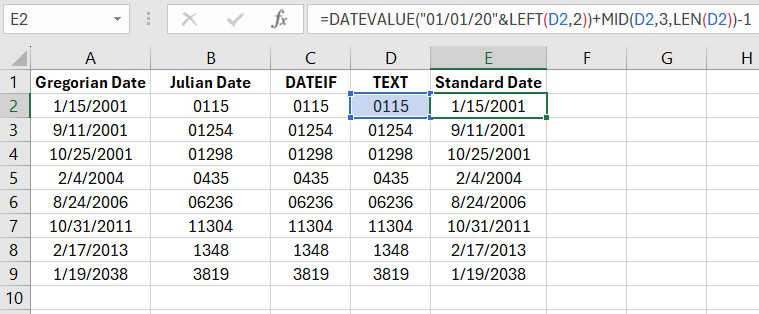
As a result, each date has been transformed into its original form, the Gregorian format - GD.

Example of Using the Julian Date Formula in Astrology

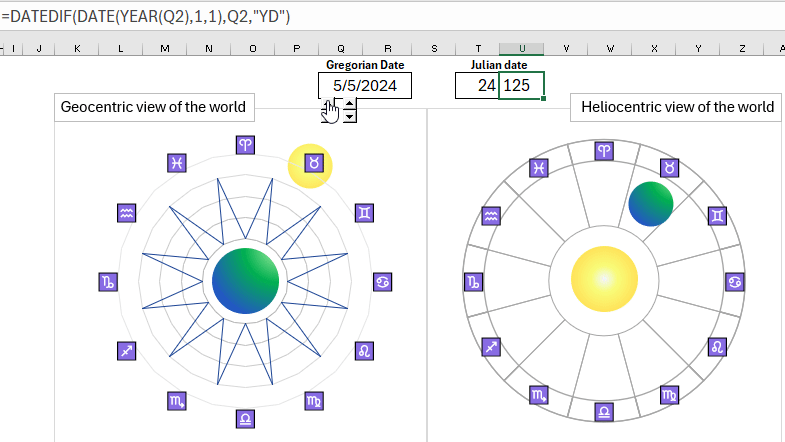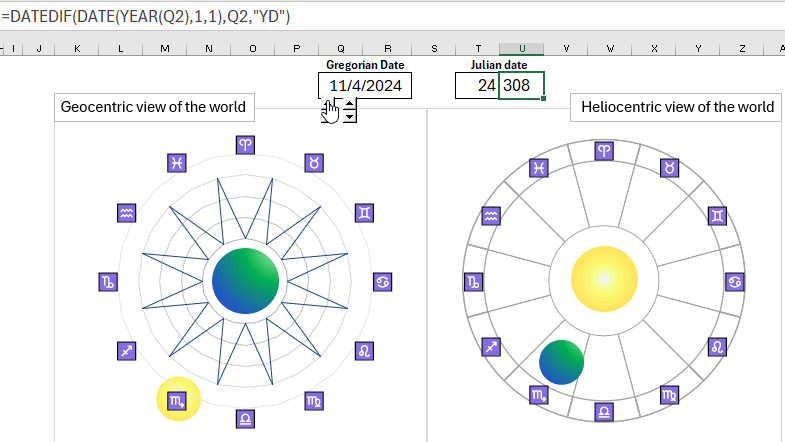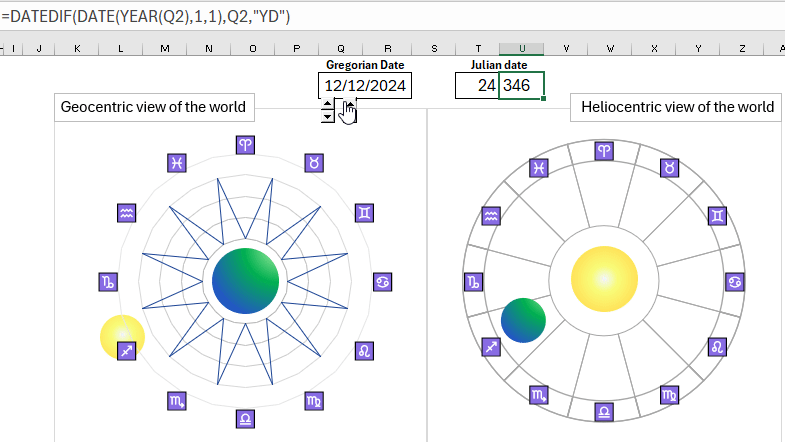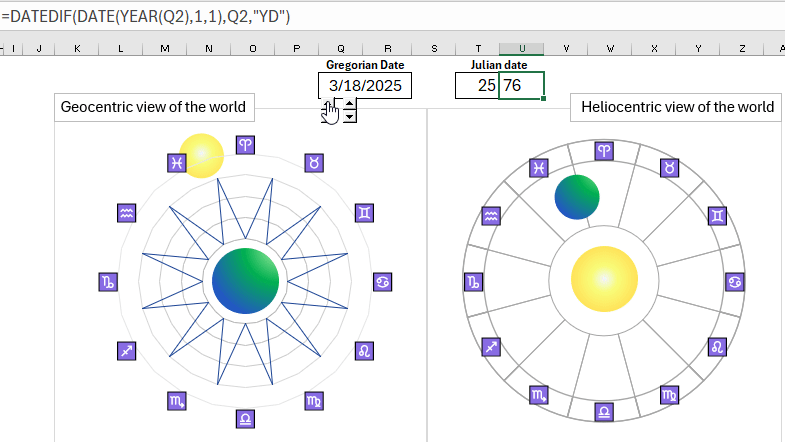
As an example, let's create an interactive mini-presentation in Excel for a comparative analysis of the geocentric and heliocentric perceptions of the world picture on the astrological zodiacal circle. The Julian date format allows for convenient implementation of interactive animation of the sun and planet movement throughout the year.

For this, we will prepare all the necessary data about the dates of zodiac signs in one table:

No	Zodiac Sign	Start Date	End Date	Icon
1	Aries	3/21/2024	4/19/2024	♈
2	Taurus	4/20/2024	5/20/2024	♉
3	Gemini	5/21/2024	6/20/2024	♊
4	Cancer	6/21/2024	7/22/2024	♋
5	Leo	7/23/2024	8/22/2024	♌
6	Virgo	8/23/2024	9/22/2024	♍
7	Libra	9/23/2024	10/22/2024	♎
8	Scorpio	10/23/2024	11/21/2024	♏
9	Sagittarius	11/22/2024	12/21/2024	♐
10	Capricorn	12/22/2024	1/20/2025	♑
11	Aquarius	1/21/2025	2/19/2025	♒
12	Pisces	1/20/2025	3/20/2025	♓

Based on this, we will create an interactive visualization of data for the presentation of the geocentric and heliocentric systems of the universe:

Introduction to the Presentation on the Role of the Calendar in Astrology

A calendar is necessary for recording periodic changes in the surrounding world. The "sense of the calendar" has always been inherent in humans and all living things in nature. This is primarily related to the alternation of seasons as a transition of weather from colder to warmer and vice versa. The formalization of this sense into certain concepts and words was apparently associated with humanity's transition from hunting and gathering, as a means of food acquisition, to agriculture and animal husbandry.

The Birth of Astrology

In ancient times, the constellations served as coordinates for the position of the Sun on the celestial sphere at the moments of its maximum elevation. It was found that each monthly shift in the Sun's position along the ecliptic (30°) corresponds to one constellation. Out of these 12 constellations, 7 were named after animals (Aries, Taurus, Cancer, Leo, Scorpio, Capricorn, and Pisces). Hence, in ancient antiquity, the entire ecliptic received the name "Zodiac" (from the ancient Greek ζῷον — 'animal'), and each of the 12 constellations became a Zodiac sign.

You may wonder how ancient astrologers determined the zodiacal constellations in which the Sun was located at the moment of its daily culmination. After all, stars are not visible during the day, especially near the Sun. However, it turns out that stars and constellations are perfectly visible from the bottom of a deep and narrow well during the day. All that was needed was to have wells dug at different angles to the Earth's surface. And when the first angular measuring instruments were invented, wells became unnecessary. At night, it was possible to determine the constellation that was in the sky at an angle measured during the day for the Sun's position at its highest point.

Geocentric and Heliocentric Models of the Universe

The geocentric (from the Greek "Earth") model of the universe postulates that the Earth is stationary and serves as the center of the cosmos. The Sun, Moon, planets, and stars revolve around it. This system, based on religious views and the works of Plato and Aristotle, was completed by the ancient Greek scholar Ptolemy (2nd century). According to the heliocentric (from the Greek "Sun") model of the universe, the Earth, rotating around its axis, is one of the planets orbiting the Sun. While individual expressions in favor of this system were present in the works of Aristarchus of Samos, Nicholas of Cusa, and others, the true creator of this theory is Copernicus, who extensively developed and mathematically substantiated it. Subsequently, Copernicus's system was refined: the Sun is located at the center not of the entire universe but only of the solar system. Galileo, Kepler, and Newton played a significant role in justifying this system. The struggle of advanced science for the victory of the heliocentric system undermined the church's doctrine of the Earth as the center of the world.

It took almost two thousand years for the geocentric system, through the efforts of Copernicus, Kepler, Galileo, and many other astronomers, to yield to the heliocentric one. And even then, not immediately. The famous "And yet it moves!" was probably thought by the great Galileo as he left the Inquisition with a promise not to speak aloud like that again.

Despite this, today we routinely use the Gregorian calendar, which is based on the geocentric model of the structure of the Universe. Originally, all calendars were based on the geocentric system, in which the Earth is stationary. Even today, it is not only a poetic image. The geocentric system is convenient for creating calendars. It is on it that the spherical astronomy is built, which introduces an imaginary sphere at a great distance from the Earth, much larger than the distance from the Earth to the Sun.

Heliocentric Julian Date

The Heliocentric Julian Date (HJD) is the Julian Date (JD) adjusted for the differences in the Earth's position relative to the Sun. During the timing of events occurring beyond the Solar System, due to the finite speed of light, the observation time of an event depends on the observer's changing position in the Solar System. Before combining multiple observations, they must be reduced to a common fixed reference location. This correction also depends on the direction to the object or event, which is calculated in time.

Julian Day

Julian Days (Julian Dates) - a system of continuous day numbering. A Julian day is equal to the number of days elapsed since Greenwich noon (12:00 GMT) on January 1, 4713 BCE, to the specified moment. Julian days are commonly denoted by the letters JD. The JD value can be a non-integer, and in such cases, it can be used to determine the moment of an event (or measure the time interval between two events) with any precision. Julian days are widely used in astronomy and chronology.

The beginning of the third millennium - midnight from December 31, 2000, to January 1, 2001 - corresponds to JD = 2,451,910.5 (meaning the first half of January 1, 2001, belongs to Julian day JD = 2,451,910, and the second half belongs to JD = 2,451,911).

Julian days were introduced by John F. Herschel in 1849 in the book "Outlines of Astronomy" based on ideas developed by the renowned historian and chronologist Joseph Scaliger (see Julian period).

The Julian Day system has two drawbacks:

1. The Julian day begins at noon, which does not align with the current civil timekeeping order, where days start at midnight.
2. The JD value corresponding to the modern epoch is very large, and the higher digits of this number do not change over observable time intervals.

The first of these issues was resolved by introducing Modified Julian Days (MJD), and the second by introducing Truncated Julian Dates with a starting point closer to the present (see Truncated Julian Dates and Lilian Day).

A continuous counting system can be linked not only to the Greenwich time scale but also to Coordinated Universal Time, International Atomic Time, Ephemeris Time, and Sidereal Time. For the same specified moment in time, all these Julian dates have different values.

Modified Julian Date

The Modified Julian Date (MJD) is related to the regular Julian Date (JD) by the following equation:

MJD = JD - 2,400,000.5.

Unlike Julian days, which begin at Greenwich noon, the start of the Modified Julian day is at midnight, aligning with the current division of time into days. Additionally, from 1859 to 2130, MJD values will be positive, and five significant digits (instead of seven for JD) will be sufficient for their representation.

The zero point of the Modified Julian Days (MJD=0) corresponds to midnight from November 16 to 17, 1858, in the Gregorian calendar.

The definition of MJD presented above is approved by the International Astronomical Union.

The Julian date format allows us to assign day numbers in a year to control the motion of the Sun or a planet in visualization:

Download

An interactive presentation helps efficiently comprehend material of any complexity. Every data designer knows there are no complex tasks, only tangled ones.