Straight-Line and Declining Balance Depreciation in Excel

Excel offers several functions to calculate depreciation: SLN, DDB, SYD, VDB, and DB. Let's look at the SLN function for calculating depreciation using the straight-line method and the VDB function for declining balance depreciation.

Depreciation in the first and last years of an asset's useful life usually differs significantly from any other year in the intermediate period. The first rule (convention) is that depreciation in the first year is not calculated for the full year, typically for half a year, month, or quarter. In the case of the half-year convention, it is assumed that the assets were acquired in the first or second half of the year, so depreciation in the current year will only be for half a year.



Formula for Straight-Line Depreciation Using the SLN Function in Excel

The figure below shows a depreciation schedule for five assets calculated using the straight-line method with the half-year convention:

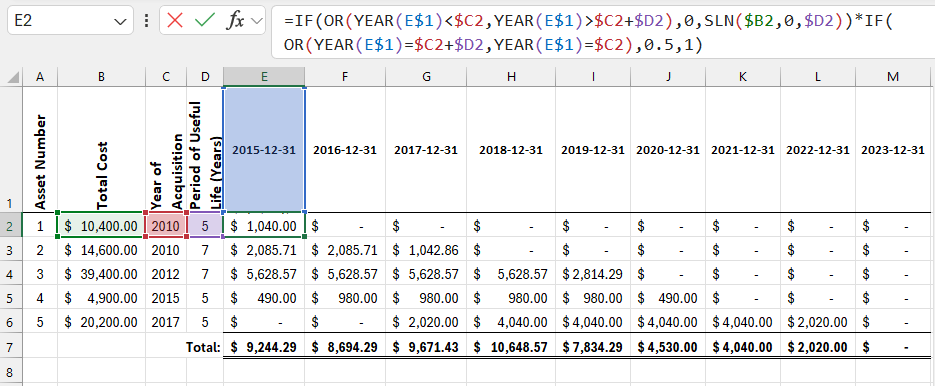
straight-line depreciation schedule.

Columns A:D contain the following user-entered data in the depreciation schedule:

  1. Asset Number – a unique identifier for each asset. It is not mandatory but can be useful for tracking assets.
  2. Total Cost – the sum of the initial cost of putting the assets into operation. It includes the purchase price, any taxes, delivery expenses, and other associated costs. This total cost is often called the "base cost."
  3. Year Acquired – the year the asset was put into service. This may differ from the year the asset was purchased and defines the start of the depreciation period.
  4. Useful Life – the estimated number of years the asset will be used.

Cells in the range E2:M6 contain the following formula:

=IF(OR(YEAR(E$1)<$C2,YEAR(E$1)>$C2+$D2),0,SLN($B2,0,$D2))*IF(OR(YEAR(E$1)=$C2+$D2,YEAR(E$1)=$C2),0.5,1)

The key part of the above formula is the SLN function =SLN($B2,0,$D2), which calculates straight-line depreciation for one period. The function has three arguments:

  1. Initial Cost.
  2. Salvage Value.
  3. Useful Life.

In this example, the salvage value is set to zero, meaning the asset will be fully depreciated at the end of its useful life.

The SLN function is simple, but since you're dealing with a depreciation schedule, some effort is needed to prepare it. The first IF function checks whether the date in the current column header is within the asset's useful life. If the date in E$1 is earlier than the asset's acquisition date $C2, the asset has not yet been put into service, and depreciation is 0. If the date is later than the acquisition date plus the useful life $D2, the asset is fully depreciated, and depreciation is also 0. These conditions are inside an OR function, so if either condition is met, the entire expression returns TRUE, and the second argument of the IF function equals 0. Otherwise, the formula returns the result of the SLN function.

The second part of the formula also uses the IF and OR functions. It determines whether the year in E$1 is the first =$C2 or last =$C2+$D2 year of depreciation. If either expression is TRUE, the depreciation calculated by the SLN function is multiplied by 0.5, following the half-year convention used in this example.

All references in the formula are mixed (partially absolute), allowing the formula to be copied to other cells. The references automatically adjust. The reference to the entire first row allows the formula to use the dates in the column headers of the Excel sheet, while references to columns B:D allow the copied formulas to use the same values for "Total Cost," "Year Acquired," and "Useful Life."

The DDB Function for Accelerated Depreciation of Assets in Excel

In the straight-line method, depreciation is calculated evenly over the asset's useful life. However, some companies use accelerated depreciation, where more depreciation occurs at the beginning of the asset's life. The theory is that an asset loses most of its value in the early years of its life. In this case, you should use the declining balance method instead of the straight-line method.

Excel provides the DDB function to calculate accelerated depreciation. This function computes depreciation for the remaining value of the asset using the double-declining balance method with an increased rate:

=IF(OR(YEAR(E$1)<$C2,YEAR(E$1)>$C2+$D2),0,DDB($B2,0,$D2,IF(YEAR(E$1)-$C2=0,1,YEAR(E$1)-$C2))*IF(OR(YEAR(E$1)=$C2+$D2,YEAR(E$1)=$C2),0.5,1))
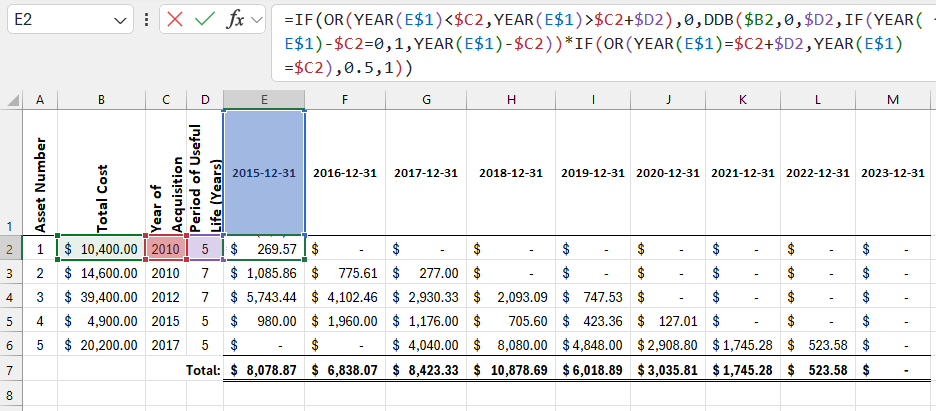
accelerated depreciation calculation.

As a result, maximum depreciation occurs in the first period, which decreases in subsequent periods. The problem with this function is that it does not depreciate the asset to zero by the end of its useful life:

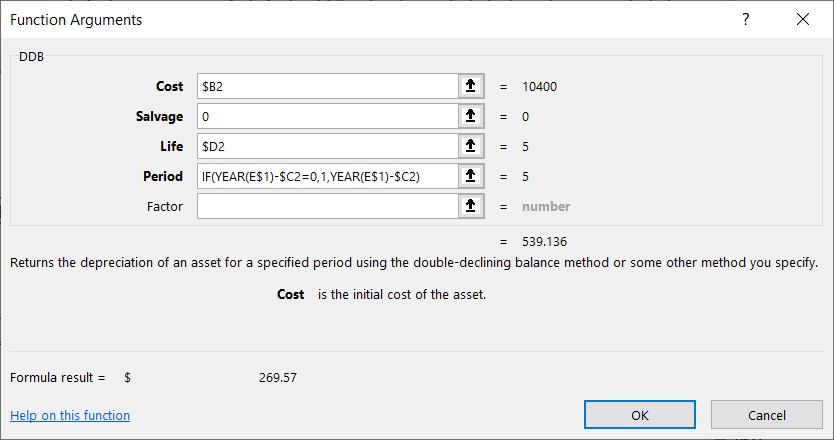
DDB function in Excel.

Thus, the depreciation decreases but never fully depreciates the asset by the end of its useful life.

VDB Function for Declining Balance Depreciation in Excel

Accelerated depreciation is most commonly applied at the beginning of an asset's life, but when the depreciation amount becomes lower than that calculated by the straight-line method, the straight-line method is applied for the remaining useful life. Excel has the VDB function that works according to this principle.

The figure below shows a depreciation schedule using the following formula:

=IF(OR(YEAR(E$1)<$C2,YEAR(E$1)>$C2+$D2),0,VDB($B2,0,$D2*2,IF(YEAR(E$1)=$C2,0,IF(YEAR(E$1)=$C2+$D2,$D2*2-1,(YEAR(E$1)-$C2)*2-1)),IF(YEAR(E$1)=$C2,1,IF(YEAR(E$1)=$C2+$D2,$D2*2,(YEAR(E$1)-$C2)*2+1))))
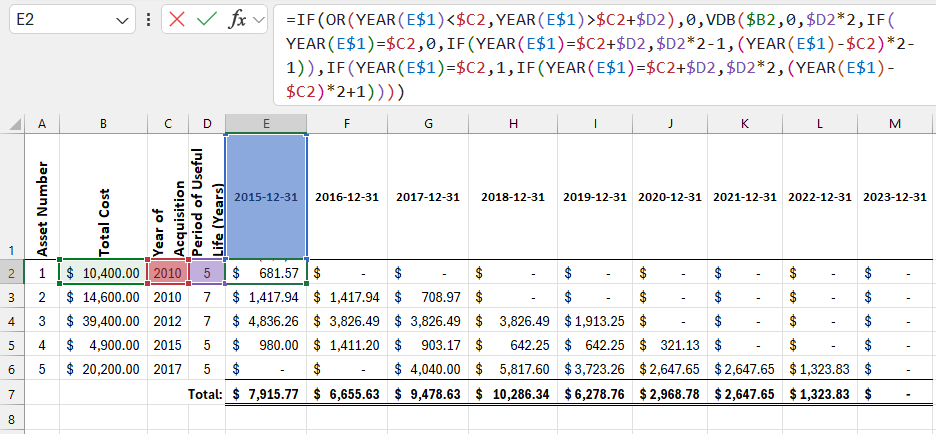
declining balance depreciation schedule.

As you can see, this formula is more complex than the one using the SLN function. However, any complex calculation can be broken down into simpler parts.

The first part of the formula is identical to the SLN formula described above. If the date in row 1 is outside the asset's useful life, depreciation is 0. Otherwise, the result of the VDB function is used as the third argument of the IF function. The VDB function includes the beginning and end of the depreciation period, which will be described below:

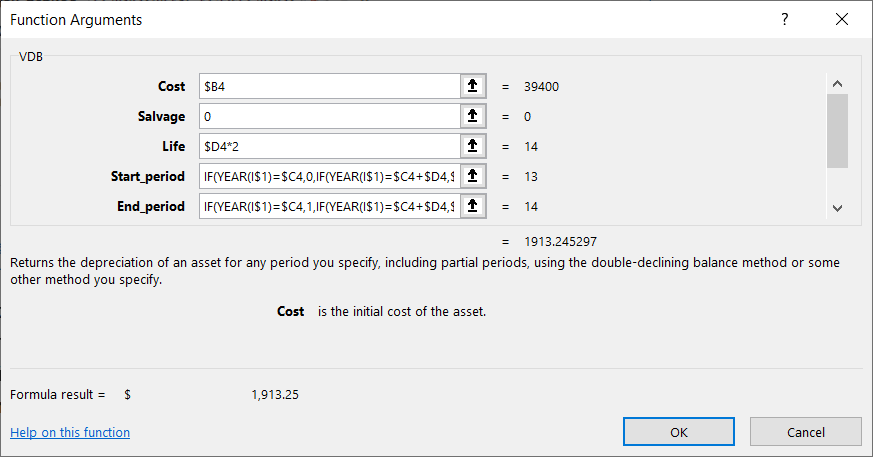
VDB function syntax.

The first three arguments of the VDB function are the same as in SLN: initial cost, salvage value, and useful life. The SLN function returns the same value for each period of depreciation, so it does not require specific periods. However, the VDB function returns different values depending on the period number. The last two arguments of the VDB function (start and end periods) define which periods are included in the calculation. The useful life in cell $D2 is doubled, which will be explained below.

No Excel function accounts for a depreciation convention. Therefore, depreciation is calculated as if all assets were acquired on the first day of the first year. In this example, the half-year convention is applied, meaning that only half of the calculated depreciation is recorded in the first and last periods. To calculate depreciation according to the half-year convention with the VDB function, you must "trick" Excel into treating the useful life as twice as long.

If the asset's useful life is five years, the first and last years are assigned periods 0 and 1, respectively. In the second year, periods 1 and 3 are used, and so on until the last year, which is represented by periods 9 and 10 (double the five-year useful life). The starting period is calculated using the following method:

  1. If the year is included and is the acquisition year, the starting period is 0.
  2. If the year is the final year, the starting period is the double useful life minus 1.
  3. In all other years, the acquisition year is subtracted from the current year, multiplied by 2, and 1 is subtracted from the result.

The formula for the end period is similar to the one for the start period. In the first year, the end period is 1, while in the final year, it is calculated as double the number of years minus 1. In other years, 1 is added (+1) instead of subtracted.

Download Excel Formulas for Straight-Line and Declining Balance Depreciation download file

For example, for an asset with a seven-year useful life, multiplying the periods by 2 applies the half-year convention with the declining balance method using the VDB function.