Функция МОПРЕД для нахождения детерминанта матрицы в Excel

Функция МОПРЕД в Excel используется для работы с прямоугольными матрицами. Задаваемыми в качестве статических массивов или диапазонов ячеек с числовыми данными, и вычисляет детерминант (определитель) исследуемой матрицы.

Матрица – математический объект, состоящий из совокупности строк из столбцов, каждый элемент которых содержит определенное числовое значение. Детерминант – один из основных вычисляемых параметров матрицы, характеризующих ее ключевые свойства.

Пример функции МОПРЕД для вычисления детерминанта матрицы в Excel

Примеры использования функции МОПРЕД в Excel.

Пример 1. Одним из свойств матриц является то, что определитель (детерминант) исходной матрицы соответствует определителю транспонированной матрицы. Доказать справедливость этого суждения с использованием средств Excel.

Вид таблицы с данными:

Исходная матрица чисел.

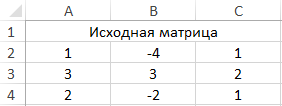
Для получения транспонированной матрицы выделим соответствующий по количеству строк и столбцов диапазон ячеек и используем следующую формулу (формула массива CTRL+SHIFT+Enter):

=ТРАНСП(A2:C4)

  • A2:A4 – диапазон ячеек со значениями исходной матрицы.

В результате получим:

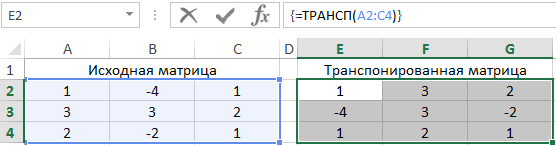
ТРАНСП.

Рассчитаем детерминант для каждой матрицы отдельно:

=МОПРЕД(A2:C4)

=МОПРЕД(E2:G4)

  • A2:C4 и E2:G4 – диапазоны ячеек со значениями исходной и транспонированной матриц соответственно.

Полученные результаты:

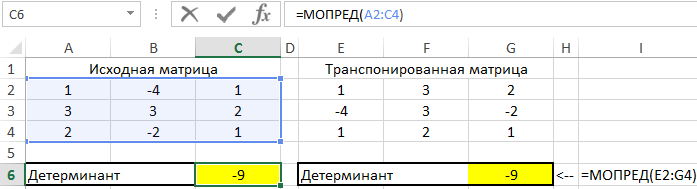
Результат примера.

Во избежание промежуточных вычислений можно было использовать формулу массива CTRL+SHIFT+Enter:

=МОПРЕД(ТРАНСП(A2:C4))

Результат вычислений:

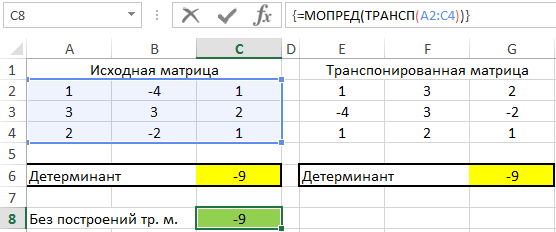
МОПРЕД.

В результате вычислений формул Excel детерминант – доказан!



Решение системы линейных уравнений по методу Крамера в Excel

Пример 2. Решить систему линейных уравнений с использованием метода Крамера. Для расчета необходимо найти определители нескольких матриц.

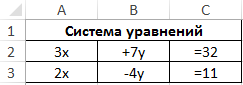
система линейных уравнений.

Вид таблицы данных:

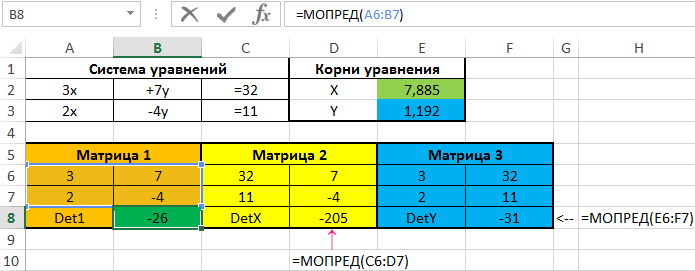
метод Крамера.

Для нахождения решений методом Крамера выделим три матрицы.

Если детерминант первой матрицы равен нулю, исходная система уравнений имеет бесконечное число решений. Проверим это условие с помощью формулы:

=МОПРЕД(A6:B7)

Результат вычислений:

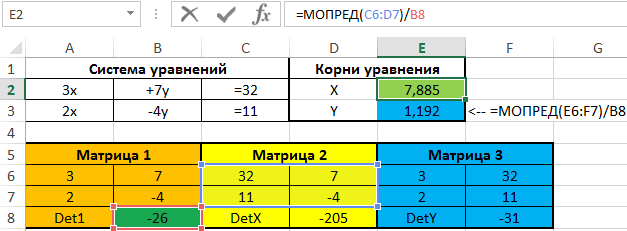
Проверка Корни уравнения.

Так как детерминант основной матрицы (Матрица 1) не равен нулю, система имеет единственное решение. Для нахождения значения переменных X и Y используем формулы:

=МОПРЕД(C6:D7)/B8

=МОПРЕД(E6:F7)/B8

Результаты вычислений:

.

Принцип работы функции МОПРЕД в Excel

Функция МОПРЕД имеет следующую синтаксическую запись:

=МОПРЕД(массив)

Единственным аргументом рассматриваемой функции является массив, который обязателен для заполнения. Он может быть указан в виде статического массива или ссылки на диапазон ячеек.

Примечания:

  1. Диапазон ячеек или статический массив должен иметь равное количество строк и столбцов, иначе результатом работы функции МОПРЕД будет код ошибки #ЗНАЧ!.
  2. Если диапазон ячеек или массив, переданные в качестве аргумента рассматриваемой функции, содержат текстовые данные или пустые значения, в результате будет возвращен код ошибки #ЗНАЧ!.
  3. Функция МОПРЕД значительно упрощает процесс расчета детерминанта матрицы. Пользователь Excel может выполнить расчеты самостоятельно. Например, для прямоугольной матрицы, значения которой находятся в диапазоне A1:C3 рассчитать детерминант можно следующим способом: A1*(B2*C3-B3*C2) + A2*(B3*C1-B1*C3) + A3*(B1*C2-B2*C1).
  4. Точность расчетов функции МОПРЕД составляет примерно 1E-16, то есть до 16 знаков после запятой. Для более точных расчетов (что требуется крайне редко) используют другие методы определения детерминанта матрицы.
  5. Значение детерминанта используют для поиска решений системы линейных уравнений.

en ru