Функции распределения ПУАССОН и ПУАССОН.РАСП в Excel

Функция ПУАССОН.РАСП в Excel используется для получения распределения Пуассона для случайных событий, происходящих за определенный промежуток времени с известной средней частотой.

Закон Пуассона распределения вероятностей случайной величины в Excel

Функция ПУАССОН.РАСП возвращает два варианта значений (в зависимости от значения, переданного в качестве третьего аргумента):

1. Интегральное распределение Пуассона – числовое значение вероятности того, что известное количество случайных событий принадлежит диапазону 0;[x] (то есть, от 0 до x включительно).
2. Функция весовых коэффициентов – числовое значение вероятности того, что количество произошедших событий точно равно числу x.

Для расчета плотности вероятности используется следующая формула:

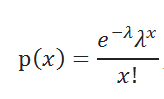
Здесь x находится в диапазоне от 0 до бесконечности со знаком плюс.

Примечания:

1. Функция распределения вероятностей (в целом) – зависимость F(x), которая в точке x принимает значение, соответствующее вероятности того, что некоторая случайная величина X будет меньше значения x), то есть F(x)=P(X<x).
2. Для понимания функций распределения вероятности рассмотрим пример о заводе по производству соков. При расфасовке тар емкостью 1000 г возможны отклонения от заявленного объема, поскольку дозирующее устройство работает с погрешностью. То есть, может быть емкость, содержащая 1000 г сока, и емкость с 980 г сока. Вероятность того, что в одной из тар будет 980 г напитка составляет 0, а 1000г – 1. Для нахождения промежуточных значений объемов используют функции распределения. К примеру, если настроить дозирующее устройство на наполнение емкостей по 990 г сока, вероятность нахождения тары с меньшим объемом напитка составляет 0,5.
3. Функция ПУАССОН использовалась в более старых версиях Excel до 2010 года. Она была оставлена для обеспечения совместимости. В более новых версиях следует использовать функцию ПУАССОН.РАСП.
4. Распределение Пуассона – один из видов функций распределения величин. Ее рационально использовать, если исследуемая математическая модель удовлетворяет следующим условиям:

• Вероятность каждого последующего события не связана с предыдущим, то есть каждое событие является независимым;
• События характеризуются средней частотой, которая является константой;
• Вероятность события и длина периода наблюдения являются пропорциональными величинами;
• Вероятность происхождения двух событий одновременна равна нулю;
• Отсчет количества событий начинается от 0 до бесконечности (0, 1, 2,…);
• Среднее значение выборки является величиной, близкой по значению к значению дисперсии.

Примечание: Распределение Пуассона неприменимо в следующих случаях:

• события являются зависимыми;
• непостоянство средней величины;
• минимальная величина превышает значение 0.



Решение задачи на распределение Пуассона в Excel

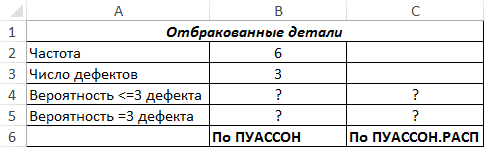
Пример 1. Отдел технического контроля определил, что среднее число не соблюденных допусков в размерах производимых деталей составляет 6. Определить вероятности следующих событий обеими рассматриваемыми функциями (для сравнения результатов вычислений):

1. Вероятность наличия 3 и менее погрешностей в случайно отобранной детали.
2. Вероятность наличия ровно 3 погрешностей в случайно выбранной детали.

Вид таблицы данных:

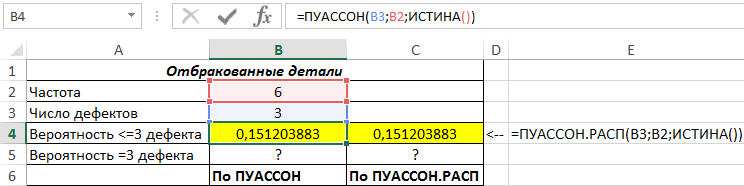
Рассчитаем вероятность наличия трех и менее дефектов с помощью функций:

=ПУАССОН(B3;B2;ИСТИНА())

=ПУАССОН.РАСП(B3;B2;ИСТИНА())

Описание аргументов:

• B3 – среднее значение;
• B2 – предполагаемое значение, для которого рассчитывается вероятность;
• ИСТИНА – указатель на интегральный тип функции.

Полученные результаты:

Для нахождения вероятности выбора детали с наличием ровно трех дефектов используем функции:

=ПУАССОН(B3;B2;ЛОЖЬ())

=ПУАССОН.РАСП(B3;B2;ЛОЖЬ())

Для расчета вероятности точного совпадения третий аргумент задан в качестве логического ЛОЖЬ.

Результаты вычислений:

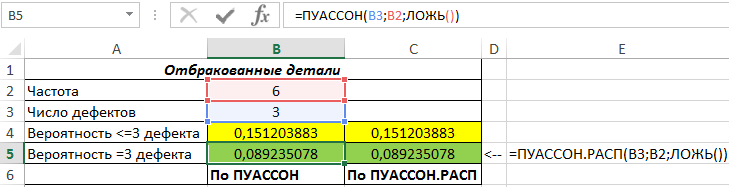
Как видно, результаты вычислений обеих функций идентичны.

Биномиальное распределение Пуассона в Excel

Пример 2. На заводе по производству мониторов ожидается, что 5% изделий будут бракованными. Была взята выборка из 30 мониторов. Определить вероятность того, что 1 монитор из 30 окажется бракованным. Для решения использовать распределение Пуассона и биномиальное распределение, полученные результаты сравнить.

Вид таблицы данных:

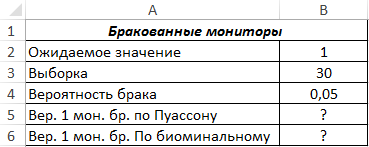
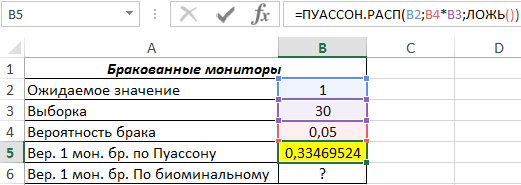
Для определения вероятности события, при котором в выборке будет найден один бракованный монитор с использованием распределения Пуассона запишем функцию:

=ПУАССОН.РАСП(B2;B4*B3;ЛОЖЬ())

Произведение B4*B3 соответствует среднему ожидаемому значению (1,5). Полученный результат:

Для расчета с использованием биномиального распределения запишем функцию:

=БИНОМ.РАСП(B2;B3;B4;ЛОЖЬ())

Результат вычислений:

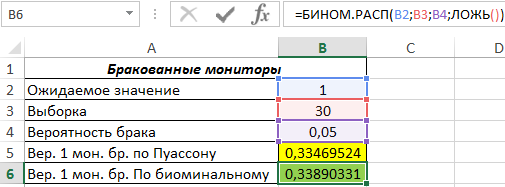
Как видно, для данной математической модели подходят оба метода определения вероятностей, поскольку полученные значения отличаются незначительно.