Примеры работы функции EXP для возведения числа Эйлера в Excel

Функция EXP в Excel используется для возведения числа Эйлера (константа e, которая примерно равна 2,718) в указанную степень и возвращает соответствующее числовое значение.

Примеры использования функции EXP в Excel

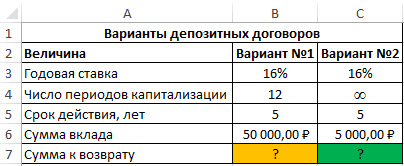
Пример 1. Вкладчику банка предложили два варианта вклада:

1. Вклад с годовой ставкой 16% и ежемесячной капитализацией.
2. Вклад с непрерывной капитализацией (число периодов капитализации – бесконечное множество за время действия депозитного договора) с годовой ставкой 16%.

Какое предложение является более выгодным? Сумма вклада – 50000 рублей, срок действия договора – 5 лет.

Вид исходной таблицы данных:

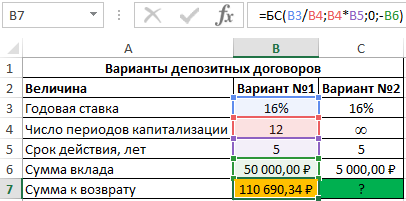
Формула для расчета будущей стоимости вклада для первого варианта депозитного договора:

=БС(B3/B4;B4*B5;0;-B6)

Во втором случае капитализация происходит непрерывно, поэтому можно воспользоваться следующей функцией:

=EXP(C3*C5)*C6

Описание аргументов:

• C3 – годовая ставка;
• C5 – срок действия договора;
• C6 – начальная сумма вклада.

Полученные результаты:

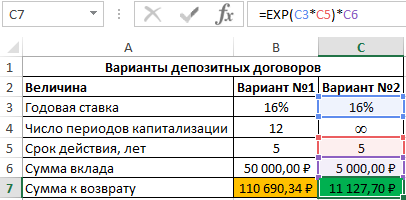
Вариант с непрерывным ростом капитализации является более выгодным.



Расчет скорости деления клеток ткани в Excel

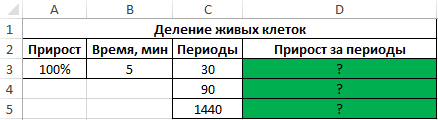
Пример 2. В начальный момент времени была только одна клетка живой материи. Каждые 5 минут такая клетка делится на 2 идентичные клетки. Определить, сколько клеток ткани образуется за 0,5 часа, 1,5 часа, сутки?

Исходная таблица имеет следующий вид:

Для расчета используем формулу массива:

=EXP(A3*C3:C5/B3)

Описание аргументов:

• A3 – прирост количества клеток (100%, то есть результатом деления одной клетки являются две новые клетки);
• C3:C5/B3 – указанные по условию периоды, деленные на время жизни клетки до окончания процесса деления.

Полученные результаты:

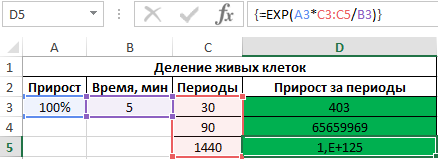
Значение 1,E+125 эквивалентно 10²⁵.

Скорость уменьшения массы радиоактивного вещества с течением времени

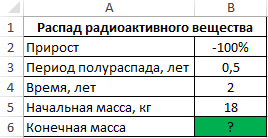
Пример 3. Количество радиоактивного вещества уменьшается вдвое за полгода. Сколько будет весить вещество спустя 2 года, если начальная масса составляла 18 кг.

Вид исходной таблицы:

Формула для расчета:

=B5*EXP(B2*B4/B3)

Описание аргументов:

• B5 – начальная масса вещества;
• B2 – прирост (отрицательное значение, поскольку количество вещества уменьшается);
• B4/B3 – количество периодов, за которые происходит полураспад.

Результат вычислений:

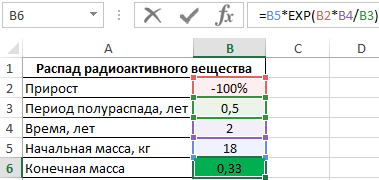
Спустя 2 года от 18 кг останется всего примерно 330 г.

Особенности использования функции EXP в Excel

Функция EXP имеет следующую синтаксическую запись:

=EXP(число)

Единственным и обязательным для заполнения аргументом является число, которое характеризует числовое значение показателя степени, в которую необходимо возвести константу e.

Примечания 1:

1. Функции LN и EXP являются противоположными друг другу по возвращаемому результату. Логарифм указывает, в какую степень необходимо возвести основание (в случае натурального логарифма lnx показатель равен примерно 2,718), чтобы получить показатель x. Функция EXP определяет показатель x.
2. Аргумент число может быть задан любым числом из диапазона действительных чисел (целые и дробные отрицательные, положительные значения и 0). Результат выполнения =EXP(0) равен 1.
3. В качестве аргумента EXP могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут автоматически преобразованы к числовым значениям 1 и 0 соответственно.
4. Если в качестве аргумента число были переданы не преобразуемые к числовому значению имя или текстовая строка, функция EXP вернет код ошибки #ЗНАЧ!.
5. Функцию можно использовать в качестве формулы массива.

Примечания 2:

1. Как известно, число e является показателем степени натурального логарифма, который записывается, например, так: ln10, то есть, логарифм с основанием 2,718 из 10. Само число e является показателем роста для любого процесса, зависимые величины которого изменяются непрерывно с изменением независимых. В качестве примеров могут служить такие процессы, как деление живых клеток организма (через определенный период времени одна клетки делится на две, затем каждая из этих двух делится еще на две и так далее) или распад радиоактивных веществ (зная коэффициент распада можно узнать, сколько радиоактивного вещества уже распалось на более простые элементы).
2. Число e используется для аппроксимации (создания упрощенной модели) систем, величины которых изменяются неравномерно.
3. Чтобы понять физический смысл числа e, рассмотрим процесс роста капиталовложений в банке. Например, банк предложил 100%-е увеличение капитала по истечению определенного периода, например, 12 месяцев. То есть, прибыль вкладчика удвоится. Предположим, что процесс роста капитала является непрерывным на протяжении года. Тогда для расчета суммы капитала по истечению 6 месяцев можно использовать формулу R=(1+100%/2)², где R – рост капитала, 2 – количество полупериодов роста. Если мы решим определить рост за 4 месяца, формула примет вид R=(1+100%/3)³, за 3 месяца - R=(1+100%/4)⁴ и т. д. В общем случае имеем формулу R=(1+100%/x)^x. Если x→∞ (стремится к бесконечности) R (рост) примет значение 2,718. Из этого следует, что максимально возможный 100%-й рост за мельчайший период времени не может превысить значение 2,718, которое и является числом e (числом Эйлера). В общем случае любой рост может быть выражен формулой R=e^p*t, где p – прирост величины (например, не 100%, как в рассмотренном выше примеров, а 30%, то есть 0,3), а t – время (например, если депозитный договор рассчитан на 5 лет, то t=5). Тогда для расчета в Excel достаточно ввести формулу =EXP(0,3*5).