Функция ФИШЕР в Excel и примеры ее работы
Функция ФИШЕР выполняет возвращение преобразования Фишера для аргументов X. Это преобразование строит функцию, которая имеет нормальное, а не асимметричное распределение. Используется функция ФИШЕР для того чтобы проверить гипотезу с помощью коэффициента корреляции.
Описание работы функции ФИШЕР в Excel
При работе с данной функцией необходимо задать значение переменной. Сразу стоит отметить, что существуют некоторые ситуации, при которых данная функция не будет выдавать результатов. Это возможно, если переменная:
- не является числом. В такой ситуации функция ФИШЕР осуществит возвращение значения ошибки #ЗНАЧ!;
- имеет значение либо меньше -1, либо больше 1. В данном случае функция ФИШЕР возвратит значение ошибки #ЧИСЛО!.
Уравнение, которое используется для математического описания функции ФИШЕР, имеет вид:
Z'=1/2*ln(1+x)/(1-x)
Рассмотрим применение данной функции на 3-x конкретных примерах.
Оценка взаимосвязи прибыли и затрат по функции ФИШЕР
Пример 1. Используя данные об активности коммерческих организаций, требуется сделать оценку связи прибыли Y (млн руб.) и затрат X (млн руб.), используемых для разработки продукции (приведены в таблице 1).
Таблица 1 – Исходные данные:
| № | X | Y |
| 1 | 210 000 000,00 ₽ | 95 000 000,00 ₽ |
| 2 | 1 068 000 000,00 ₽ | 76 000 000,00 ₽ |
| 3 | 1 005 000 000,00 ₽ | 78 000 000,00 ₽ |
| 4 | 610 000 000,00 ₽ | 89 000 000,00 ₽ |
| 5 | 768 000 000,00 ₽ | 77 000 000,00 ₽ |
| 6 | 799 000 000,00 ₽ | 85 000 000,00 ₽ |
Схема решения таких задач выглядит следующим образом:
- Рассчитывается линейный коэффициент корреляции rxy;
- Проверяется значимость линейного коэффициента корреляции на основе t-критерия Стьюдента. При этом выдвигается и проверяется гипотеза о равенстве коэффициента корреляции нулю. При проверке этой гипотезы используется t-статистика. Если гипотеза подтверждается, t-статистика имеет распределение Стьюдента. Если расчетное значение tр > tкр, то гипотеза отвергается, что свидетельствует о значимости линейного коэффициента корреляции, а следовательно, и о статистической существенности зависимости между Х и Y;
- Определяется интервальная оценка для статистически значимого линейного коэффициента корреляции.
- Определяется интервальная оценка для линейного коэффициента корреляции на основе обратного z-преобразования Фишера;
- Рассчитывается стандартная ошибка линейного коэффициента корреляции.
Результаты решения данной задачи с применяемыми функциями в пакете Excel приведены на рисунке 1.
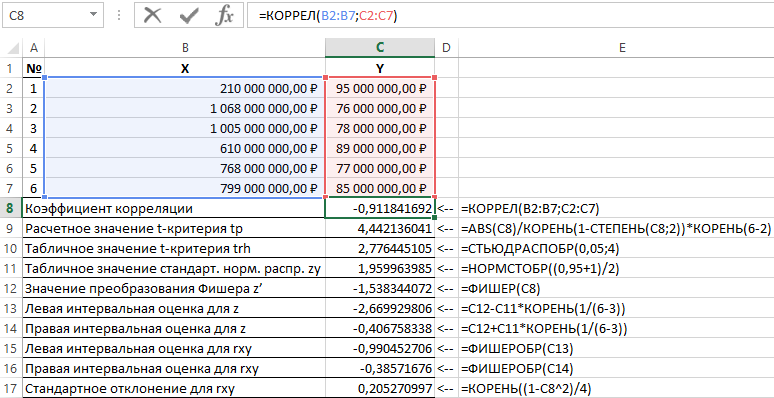
Рисунок 1 – Пример расчетов.
| № п/п | Наименование показателя | Формула расчета |
| 1 | Коэффициент корреляции | =КОРРЕЛ(B2:B7;C2:C7) |
| 2 | Расчетное значение t-критерия tp | =ABS(C8)/КОРЕНЬ(1-СТЕПЕНЬ(C8;2))*КОРЕНЬ(6-2) |
| 3 | Табличное значение t-критерия trh | =СТЬЮДРАСПОБР(0,05;4) |
| 4 | Табличное значение стандартного нормального распределения zy | =НОРМСТОБР((0,95+1)/2) |
| 5 | Значение преобразования Фишера z’ | =ФИШЕР(C8) |
| 6 | Левая интервальная оценка для z | =C12-C11*КОРЕНЬ(1/(6-3)) |
| 7 | Правая интервальная оценка для z | =C12+C11*КОРЕНЬ(1/(6-3)) |
| 8 | Левая интервальная оценка для rxy | =ФИШЕРОБР(C13) |
| 9 | Правая интервальная оценка для rxy | =ФИШЕРОБР(C14) |
| 10 | Стандартное отклонение для rxy | =КОРЕНЬ((1-C8^2)/4) |
Таким образом, с вероятностью 0,95 линейный коэффициент корреляции заключен в интервале от (–0,386) до (–0,990) со стандартной ошибкой 0,205.
Проверка статистической значимости регрессии по функции FРАСПОБР
Пример 2. Произвести проверку статистической значимости уравнения множественной регрессии с помощью F-критерия Фишера, сделать выводы.
Для проверки значимости уравнения в целом выдвинем гипотезу Н0 о статистической незначимости коэффициента детерминации и противоположную ей гипотезу Н1 о статистической значимости коэффициента детерминации:
Н0: R2 = 0;
Н1: R2 ≠ 0.
Проверим гипотезы с помощью F-критерия Фишера. Показатели приведены в таблице 2.
Таблица 2 – Исходные данные
| Показатель | SS | MS | Fрасч |
| Регрессия | 454,814 | 227,407 | 7,075 |
| Остаток | 1607,014 | 32,14 | |
| Итого | 2061,828 | - |
Для этого используем в пакете Excel функцию:
=FРАСПОБР (α;p;n-p-1)
где:
- α – вероятность, связанная с данным распределением;
- p и n – числитель и знаменатель степеней свободы, соответственно.
Зная, что α = 0,05, p = 2 и n = 53, получаем следующее значение для Fкрит (см. рисунок 2).
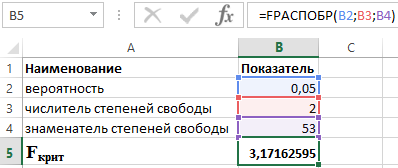
Рисунок 2 – Пример расчетов.
Таким образом можно сказать, что Fрасч > Fкрит. В итоге принимается гипотеза Н1 о статистической значимости коэффициента детерминации.
Расчет величины показателя корреляции в Excel
Пример 3. Используя данные 23 предприятий о: X - цена на товар А, тыс. руб.; Y — прибыль торгового предприятия, млн. руб, производится изучение их зависимости. Оценка регрессионной модели дала следующее: ∑(yi-yx)2 = 50000; ∑(yi-yср)2 = 130000. Какой показатель корреляции можно определить по этим данным? Рассчитайте величину показателя корреляции и, используя критерий Фишера, сделайте вывод о качестве модели регрессии.
Определим Fкрит из выражения:
Fрасч = R2/23*(1-R2)
где R – коэффициент детерминации, равный 0,67.
Таким образом, расчетное значение Fрасч = 46.
Для определения Fкрит используем распределение Фишера (см. рисунок 3).
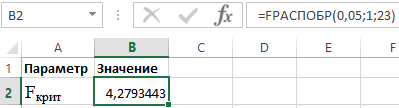
Рисунок 3 – Пример расчетов.
Скачать примеры работы функции ФИШЕР в Excel
Таким образом, полученная оценка уравнения регрессии надежна.