Функции СТАНДОТКЛОН.В, СТАНДОТКЛОН.Г, СТАНДОТКЛОНА и СТАНДОТКЛОНПА в Excel

Функция СТАНДОТКЛОН.В возвращает значение стандартного отклонения, рассчитанного для определенного диапазона числовых значений.

Функция СТАНДОТКЛ.Г используется для определения стандартного отклонения генеральной совокупности числовых значений и возвращает величину стандартного отклонения с учетом, что переданные значения являются всей генеральной совокупностью, а не выборкой.

Функция СТАНДОТКЛОНА возвращает значение стандартного отклонения для некоторого диапазона чисел, которые являются выборкой, а не всей генеральной совокупностью.

Функция СТАНДОТЛОНПА возвращает значение стандартного отклонения для всей генеральной совокупности, переданной в качестве ее аргументов.

Примеры использования СТАНДОТКЛОН.В, СТАНДОТКЛОН.Г, СТАНДОТКЛОНА и СТАНДОТКЛОНПА

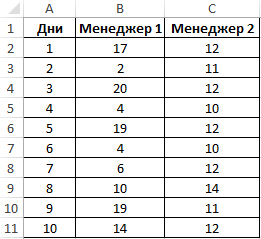
Пример 1. На предприятии работают два менеджера по привлечению клиентов. Данные о количестве обслуженных клиентов в день каждым менеджером фиксируются в таблице Excel. Определить, какой из двух сотрудников работает эффективнее.

Таблица исходных данных:

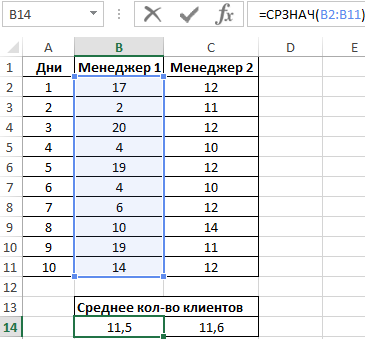
Вначале рассчитаем среднее количество клиентов, с которыми работали менеджеры ежедневно:

=СРЗНАЧ(B2:B11)

Данная функция выполняет расчет среднего арифметического значения для диапазона B2:B11, содержащего данные о количестве клиентов, принимаемых ежедневно первым менеджером. Аналогично рассчитаем среднее количество клиентов за день у второго менеджера. Получим:

На основе полученных значений создается впечатление, что оба менеджера работают примерно одинаково эффективно. Однако визуально виден сильный разброс значений числа клиентов у первого менеджера. Произведем расчет стандартного отклонения по формуле:

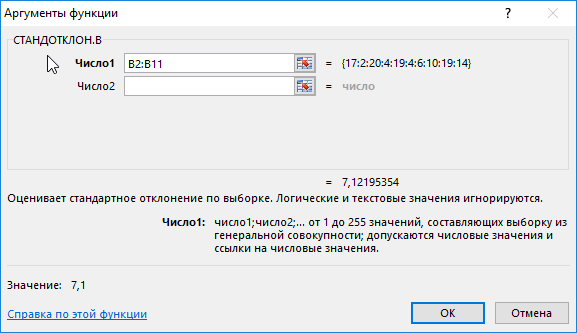
=СТАНДОТКЛОН.В(B2:B11)

B2:B11 – диапазон исследуемых значений. Аналогично определим стандартное отклонение для второго менеджера и получим следующие результаты:

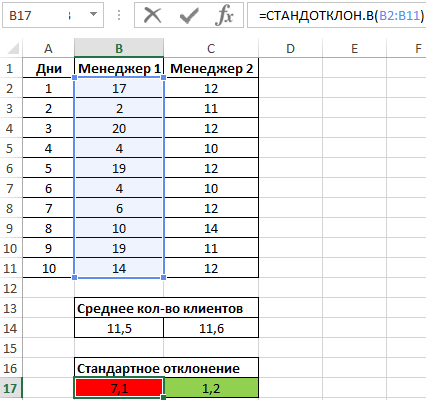
Как видно, показатели работы первого менеджера отличаются высокой вариабельностью (разбросом) значений, в связи с чем среднее арифметическое значение абсолютно не отражает реальную картину эффективности работы. Отклонение 1,2 свидетельствует о более стабильной, а, значит, и эффективной работе второго менеджера.

Пример использования функции СТАНДОТКЛОНА в Excel

Пример 2. В двух различных группах студентов колледжа проводился экзамен по одной и той же дисциплине. Оценить успеваемость студентов.

Таблица исходных данных:

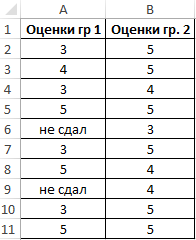
Определим стандартное отклонение значений для первой группы по формуле:

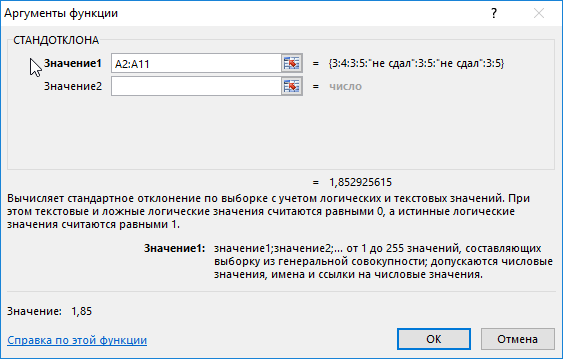
=СТАНДОТКЛОНА(A2:A11)

Аналогичный расчет произведем для второй группы. В результате получим:

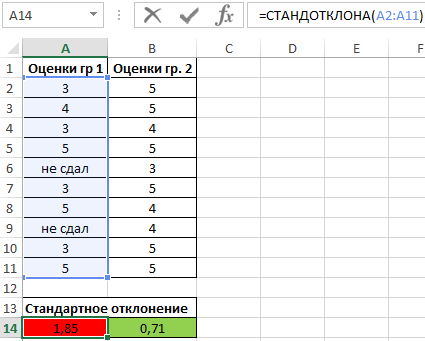
Полученные значения свидетельствуют о том, что студенты второй группы намного лучше подготовились к экзамену, поскольку разброс значений оценок относительно небольшой. Обратите внимание на то, что функция СТАНДОТКЛОНА преобразует текстовое значение «не сдал» в числовое значение 0 (нуль) и учитывает его в расчетах.

Пример функции СТАНДОТКЛОН.Г в Excel

Пример 3. Определить эффективность подготовки студентов к экзамену для всех групп университета.

Примечание: в отличие от предыдущего примера, будет анализироваться не выборка (несколько групп), а все число студентов – генеральная совокупность. Студенты, не сдавшие экзамен, не учтены.

Заполним таблицу данных:

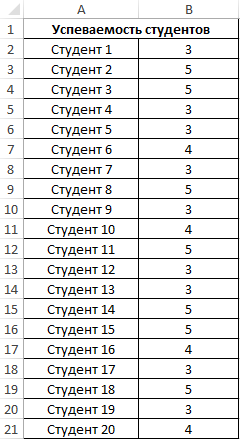
Для оценки эффективности будем оперировать двумя показателями: средняя оценка и разброс значений. Для определения среднего арифметического используем функцию:

=СРЗНАЧ(B2:B21)

Для определения отклонения введем формулу:

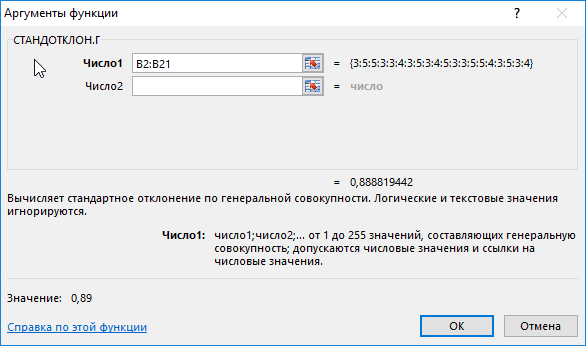
=СТАНДОТКЛОН.Г(B2:B21)

В результате получим:

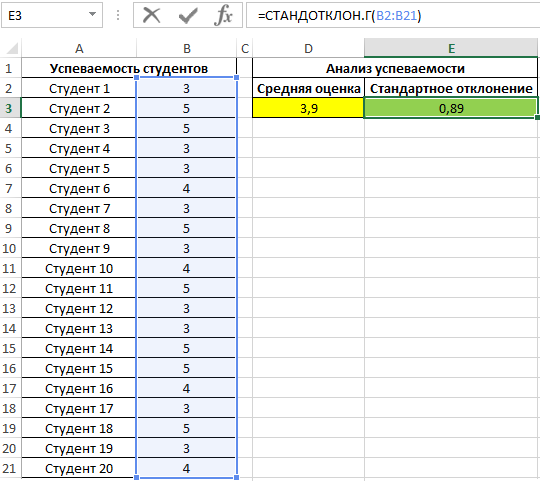
Полученные данные свидетельствует об успеваемости немного ниже среднего (<4), величина разброса характеризует довольно большое количество студентов, получивших 5 и 3 соответственно (учитывая, что анализировались только данные из диапазона от 3 до 5).

Пример функции СТАНДОТКЛОНПА в Excel

Пример 4. Проанализировать успеваемость студентов по результатам сдачи экзамена с учетом тех студентов, которым не удалось сдать этот экзамен.

Таблица данных:

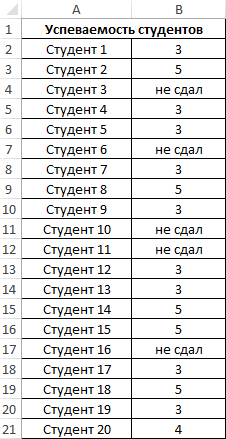
В данном примере также анализируем генеральную совокупность, однако некоторые поля данных содержат текстовые значения. Для определения стандартного отклонения используем функцию:

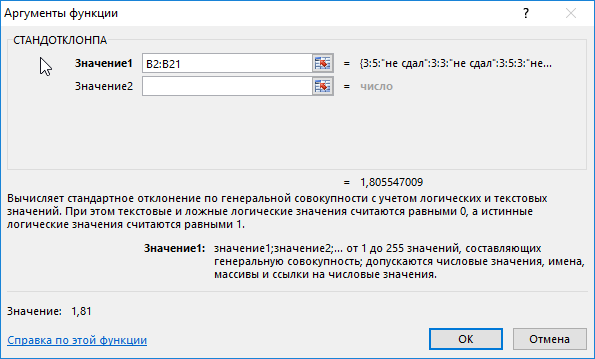
=СТАНДОТКЛОНПА(B2:B21)

В результате получим:

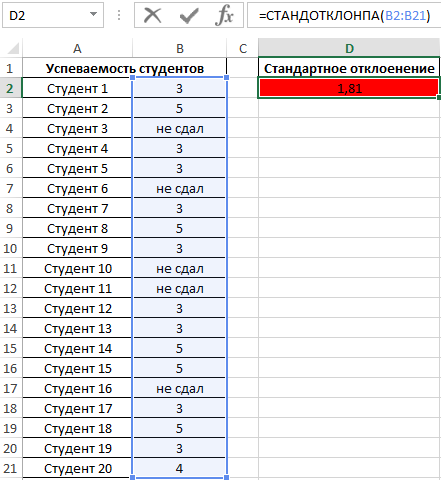
Высокий разброс значений в последовательности свидетельствует о большом числе не сдавших экзамен студентов.

Особенности использования СТАНДОТКЛОН.В, СТАНДОТКЛОН.Г, СТАНДОТКЛОНА и СТАНДОТКЛОНПА

Функции СТАНДОТКЛОНА И СТАНДОТКЛОНПА имеют идентичную синтаксическую запись типа:

=ФУНКЦИЯ (значение1; [значение2];…)

Описание:

ФУНКЦИЯ – одна из двух рассмотренных выше функций;
значение1 – обязательный аргумент, характеризующий одно из значений выборки (либо генеральной совокупности);
[значени2] – необязательный аргумент, характеризующий второе значение исследуемого диапазона.

Примечания:

В качестве аргументов функций могут быть переданы имена, числовые значения, массивы, ссылки на диапазоны числовых данных, логические значения и ссылки на них.
Обе функции игнорируют пустые значения и текстовые данные, содержащиеся в диапазоне переданных данных.
Функции возвращают код ошибки #ЗНАЧ!, если в качестве аргументов были переданы значения ошибок или текстовые данные, которые не могут быть преобразованы в числовые значения.

Функции СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г имеют следующую синтаксическую запись:

=ФУНКЦИЯ(число1;[число2];…)

Описание:

ФУНКЦИЯ – любая из функций СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г;
число1 – обязательный аргумент, характеризующий числовое значение, взятое из выборки или всей генеральной совокупности;
число2 – необязательный аргумент, характеризующий второе числовое значение исследуемого диапазона.

Примечание: обе функции не включают в процесс вычисления числа, представленные в виде текстовых данных, а также логические значения ИСТИНА и ЛОЖЬ.

Примечания:

Стандартное отклонение широко используется в статистических расчетах, когда нахождение среднего значения диапазона величин не дает верное представление о распределении данных. Оно демонстрирует принцип распределения величин относительно среднего значения в конкретной выборке или всей последовательности целиком. В Примере 1 будет наглядно рассмотрено практическое применение данного статистического параметра.
Функции СТАНДОТКЛОНА и СТАНДОТКЛОН.В следует использовать для анализа только части генеральной совокупности и производят расчет по первой формуле, а СТАНДОТКЛОН.Г и СТАНДОТКЛОНПА должны принимать на вход данные о всей генеральной совокупности и производят расчет по второй формуле.
В Excel содержатся встроенные функции СТАНДОТКЛОН и СТАНДОТКЛОНП, оставленные для совместимости с более старыми версиями Microsoft Office. Они могут быть не включены в более поздние версии программы, поэтому их использование не рекомендуется.
Для нахождения стандартного отклонения используются две распространенные формулы: S=√((∑_(i=1)^n▒(x_i-x_ср )^2 )/(n-1)) и S=√((∑_(i=1)^n▒(x_i-x_ср )^2 )/n), где:

S – искомое значение стандартного отклонения;
n – рассматриваемый диапазон значений (выборка);
x_i – отдельно взятое значение из выборки;
x_ср – среднее арифметическое значение для рассматриваемого диапазона.