Примеры решений распределения с помощью функции ГАУСС в Excel
Функция ГАУСС, подлежащая применению в версиях Excel начиная от 2013 года или новее. Она позволяет вычислить такую вероятность, с которой элемент стандартной нормальной совокупности будет находиться в интервале между средними и стандартными отклонениями от среднего.
Примеры использования функции ГАУСС в Excel
Синтаксис рассматриваемой функции не представляет из себя ничего сложного, ведь функции ГАУСС присущ всего один обязательный аргумент – Z – возвращающий число.
Важно отметить, что существует определенная связь между функцией ГАУСС и такой статистической функцией, как стандартное нормальное распределение, иначе говоря – НОРМ.СТ.РАСП.
Итак, всегда функция НОРМ.СТ.РАСП (0; Истина) делает возврат 0,5, тогда как ГАУСС (z) имеет в результате значение меньше на 0,5, чем результат функции НОРМ.СТ.РАСП. На рисунке, расположенном ниже, приведен пример использования данных статистических функций для возвращения числа 1,5.

Для наглядности продемонстрируем зависимость между значениями функций графическим способом. Для этого – сформируем таблицу с выборкой чисел, например на интервале от -5 до 5 с шагом 0,5, а затем по имеющимся данным построим график:
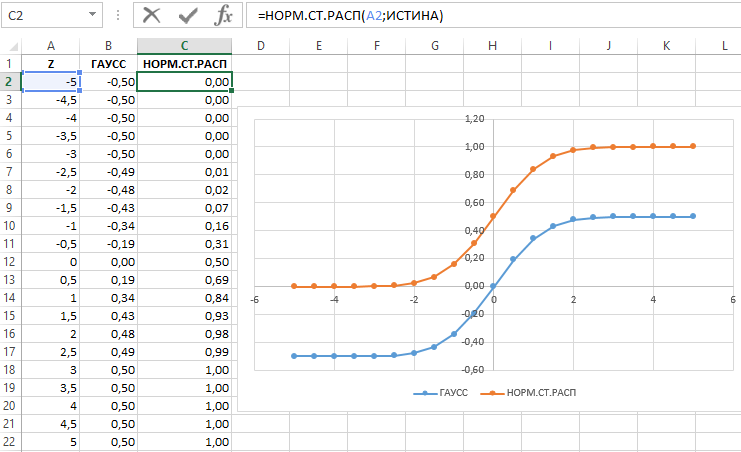
На графике четко прослеживается пропорциональная корреляция результатов вычислений функций ГАУСС и НОРМ.СТ.РАСП.
Решение системы вероятности методом ГАУССА в Excel
Задача представляет собой вычисление вероятности возможных значений при бросании двух костей.
Пример с игрой в кости является наиболее наглядным, так как мы имеем ограниченный набор данных, которые соответствуют вероятностям. Так, вероятность имеет значение от нуля до единицы, к которому стремится наблюдаемая частота при бесконечно большой выборке или повторении эксперимента.
Существует 36 возможных комбинаций. При этом, вероятность того, что при бросании двух костей выпадет 2 очка равна 1/36, а 7 очков – 1/6. Отобразим перечень возможных значений бросания двух игральных костей в таблице, приведя при этом все вероятности к общему знаменателю.
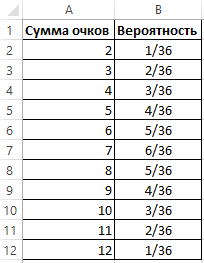
Однако, такой ряд данных не дает возможности для выявления полного распределения, поэтому следует отобразить данные об отдельных вероятностях в рассчитанную по функции распределения. Так необходимо, все вероятности просуммировать последовательно (1+2+3+4+5+6+5+4+3+2+1).
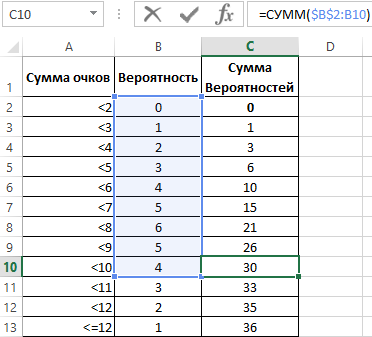
Теперь определяем коэффициент вероятности разделив по отдельности последовательную сумму вероятностей на максимально возможное количество комбинаций 36.
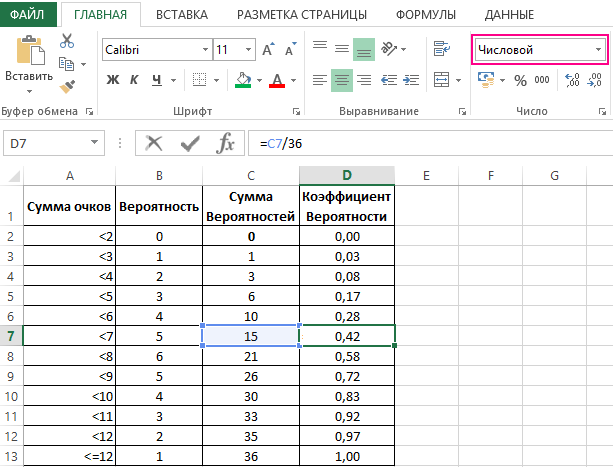
В первом случае нами были рассмотрены отдельные вероятности, во втором – сумма вероятностей от первого возможного значения до заданного.
Необходимо преобразовать диапазон ячеек D2:D13 в числовой формат данных, иначе при обращении на них функции ГАУСС будет иметь место ошибка.
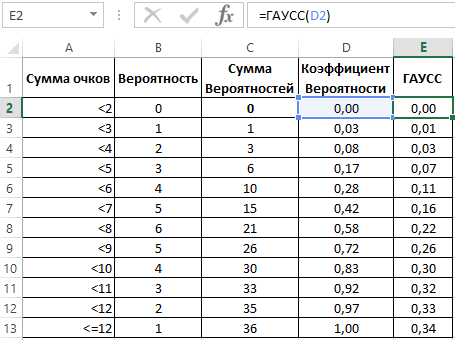
В созданный рядом с первоначальной таблицей столбец E введем формулу, которая в качестве аргумента делает обращение к ячейке D2.
Далее, протянем формулу вниз по столбцу, и получим ряд вероятностей с использованием функции ГАУСС.
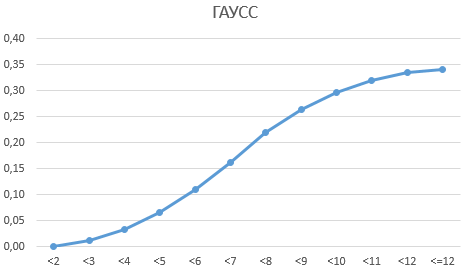
Для более наглядной визуализации, построим график вероятности:
Решение вероятности методом распределения кривой Гаусса в Excel
Теперь в качестве примера нормального распределения с помощью функции ГАУСС решим задачу о вероятностном соотношении результатов стрельбы по мишени.
Для этого построим базовую таблицу, которая отражает результаты стрельбы по мишени в девяти подходах.
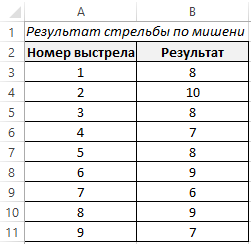
Затем, выберем только уникальные результаты, для этого используем хитрую формулу:
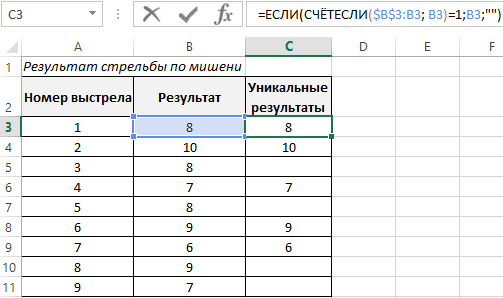
Делаем сортировку формулой для результатов по возрастанию и выводим в отдельную табличку:
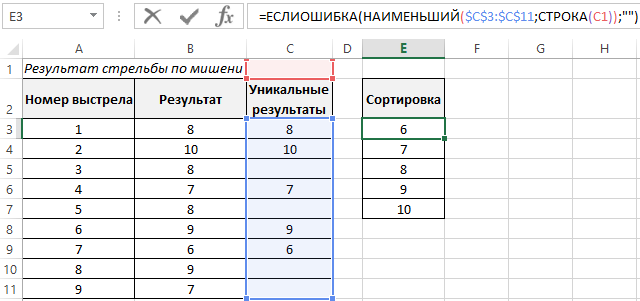
После чего определим частоту встречающихся только для уникальных результатов:
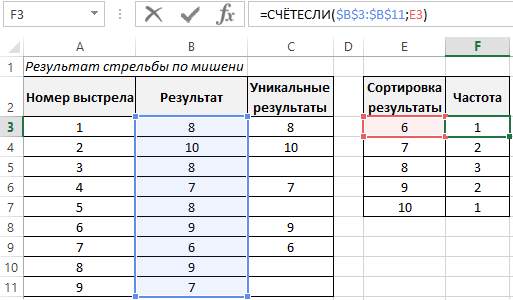
Далее применим функцию ГАУСС к значениям ячеек с частотой встречаемости. Отразим результаты вычислений на графике:
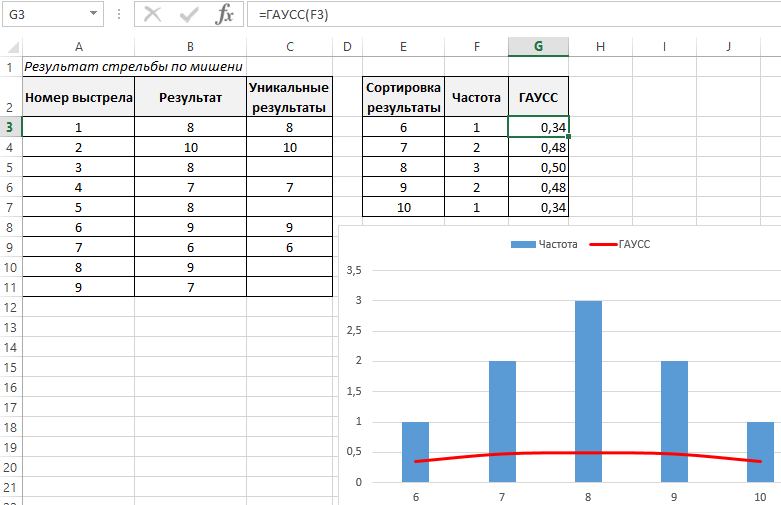
На графике красной линией определено нормальное распределение кривой Гаусса.