FРАСПОБР для проверки значимости модели регрессии в Excel

Функция FПАСПОБР в Excel используется для проверки значимости модели регрессии с применением F-критерия (критерий Фишера), и возвращает числовое значение, соответствующее обратному значению для F-распределения вероятностей (верхнему квантилю). Например, если в качестве вероятности (первый аргумент функции) было введено значение уровня значимости, к примеру, 0,08, то FПАСПОБР вычислит значение случайной величины x, для которой выполняется следующее условие – P(X>x) = 0,08.

Функция FРАСПОБР для оценки значимости параметров модели регрессии

Критическое значения F может быть определено в случае, если в качестве первого аргумента рассматриваемой функции будет введено значение уровня значимости.

Для расчета F используется следующая формула:

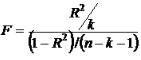
оценки значимости параметров модели.

Функция оперирует двумя дополнительными критериями:

  1. Числитель степеней свободы: n1 = k.
  2. Знаменатель степеней свободы: n2 = (n – k – 1).

Через переменную k обозначают число факторов, которые были включены в исследуемую модель регрессии.

В Excel предусмотрена функция для расчета вероятности для распределения Фишера – FРАСП. Между данной и рассматриваемой функциями существует следующая взаимосвязь: =FРАСПОБР(FРАСП(x;n1;n2);n1;n2)=x.

Примечание:

В MS Office 2007 и более поздних версиях была введена функция F.ОБР.ПХ, которая заменила рассматриваемую функцию. FПАСПОБР была оставлена для обеспечения совместимости с документами, созданными в более старых версиях Excel.



Определение верхнего квартиля F-распределения Фишера в Excel

Пример 1. В таблице указаны вероятность, связанная с распределением Фишера, а также числитель и знаменатель степеней свободы соответственно. Определить верхний квантиль данного F-распределения.

Вид таблицы данных:

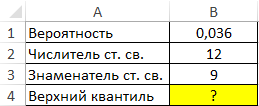
Пример 1.

Вычислим искомое значение с помощью функции:

=FРАСПОБР(B1;B2;B3)

Полученное число:

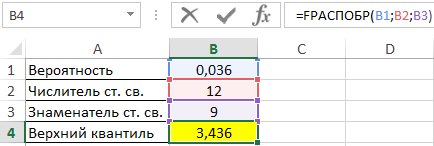
FРАСПОБР.

Оценка в Excel эффективности использования технологий на производстве

Пример 2. На заводе есть несколько цехов по производству одного типа продукции. Существует 3 различные технологии изготовления данной продукции. Для оценки были записаны данные о количестве часов, необходимых для производства одной партии продукции каждым цехом с использованием каждой из трех технологий. Оценить эффективность использования технологий, проанализировать полученные значения.

Вид таблицы данных:

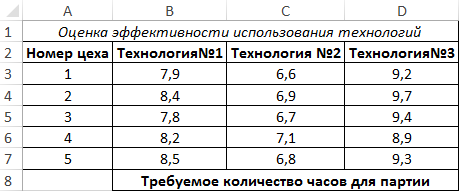
Пример 2.

Проведем однофакторный дисперсионный анализ для данных, находящихся в диапазоне ячеек B3:D7, используя соответствующую надстройку Excel. Полученная таблица результатов:

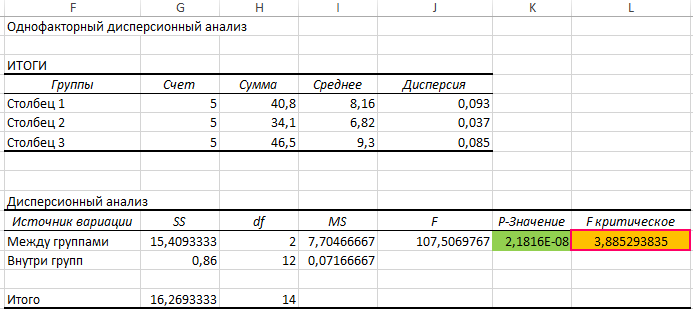
однофакторный дисперсионный анализ данных.

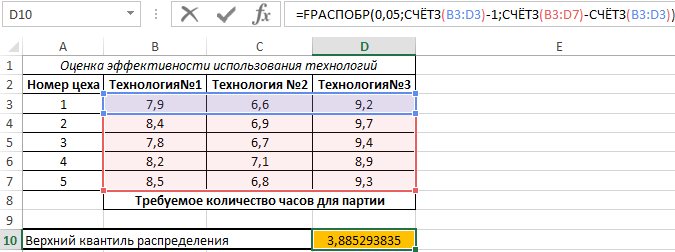
По условия поставленной задачи нас интересует выделенное значение. Поскольку оно <0,05, между данными существует линейная зависимость. В результате анализа уже было определено значение, возвращаемое функцией FРАСПОБР (F критическое). Для расчета можно было использовать функцию:

Здесь СЧЁТЗ(B3:D3) определяет число полей данных, а СЧЁТЗ(B3:D7) – количество исследуемых числовых значений.

Полученное число:

Оценка эффективности технологий.

Особенности использования функции FРАСПОБР в Excel

Функция имеет следующую синтаксическую запись:

=FРАСПОБР(вероятность;степени_свободы1;степени_свободы2)

Описание аргументов:

  • вероятность – обязательный, принимает числовое значение, характеризующее вероятность, которая связана с распределением Фишера;
  • степени_свободы1 – обязательный, принимает числовое значение, соответствующее числителю степеней свободы (равно числу факторов исследуемой регрессии);
  • степени_свободы2 – обязательный, принимает числовое значение, соответствующее знаменателю степеней свободы.

Примечания:

  1. Рассматриваемая функция принимает в качестве любого из аргументов только числовые значения и данные, которые могут быть преобразованы к числам. Если любой из аргументов принимает данные недопустимого типа, будет сгенерирован код ошибки #ЗНАЧ!
  2. Первый аргумент должен быть задан числом из диапазона от 0 до 1. В противном случае функция FПАСПОБР вернет код ошибки #ЧИСЛО!
  3. Второй и третий аргумент функции должны быть заданы числами из диапазона от 1 до 10^10. При вводе значений, находящихся вне допустимого диапазона, будет сгенерирован код ошибки #ЧИСЛО!
  4. Рассматриваемая функция использует итеративный подход к вычислениям (последовательный подбор приближенного значения в циклах). Если спустя 100 итераций решение не было найдено, результатом выполнения функции FПАСПОБР будет код ошибки #Н/Д.

en ru