Функция ВЕЙБУЛЛ для расчета распределения Вейбулла в Excel

Функция ВЕЙБУЛЛ в Excel предназначена для определения интегральной функции распределения Вейбулла, а также плотность вероятности (в зависимости от значения, переданного в качестве последнего аргумента), и возвращает соответствующее числовое значение.

Коэффициенты и параметры функции распределения по закону Вейбулла

Интегральная функция распределения соответствует значению вероятности события, при котором некоторая величина X, распределенная по закону Вейбулла, будет принимать значение, которое <=x.

Формула функции ВЕЙБУЛЛ:

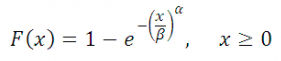
Формула плотности вероятности для данного распределения:

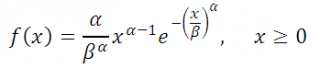
Данное распределение характеризуется двумя основными параметрами:

1. α - характеризует форму распределения.
2. β - характеризует масштаб.

Оба параметра указываются значениями из диапазона от 0 (не включительно) до бесконечности со знаком плюс (при этом для практического применения распределения рационально в качестве параметра β (бетта) указывать значение >=1).

Распределение Вейбулла может быть преобразовано к обычному экспоненциальному распределению, если параметр α (альфа) принимает значение 1.

Целесообразность применения:

1. Определение времени наработки без отказа до момента выхода из строя самого уязвимого элемента системы.
2. Определение времени работы до момента разрушения вследствие внутренних причин (физический износ материала). Если причина разрушения материала обусловлена внешними факторами, применяют экспоненциальное распределение (то есть, принимают α=1).

Примечание:

Рассматриваемая функция использовалась до выхода MS Office версии 2010 года. В последующих версиях она заменена аналогичной функцией ВЕЙБУЛЛ.РАСП, однако оставлена для обеспечения совместимости.



Плотность распределения Вейбулла в Excel

Пример 1. Определить интегральную функцию распределения Вейбулла и функцию плотности вероятности для некоторого значения x=85, если данная величина подчиняется закону распределения Вейбулла с α-параметром равным 17 и β-параметром равным 90.

Вид таблицы данных:

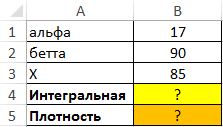
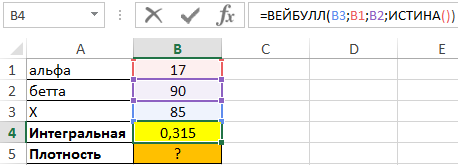
Для определения первого значения используем следующую запись:

Четвертый аргумент принимает значение ИСТИНА для расчета интегральной функции. Полученный результат:

Аналогичность определим функцию плотности:

Результат расчета:

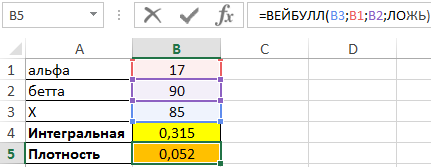
В результате с помощью одной функции мы вычислили 2 коэффициента в Excel.

Распределение Вейбулла случайной величины в Excel

Пример 2. Сгенерировать 10 случайных величин, имеющих распределение Вейбулла. Определить интегральные значения при известных альфа- и бета-параметрах (8 и 35 соответственно).

Вид таблицы данных:

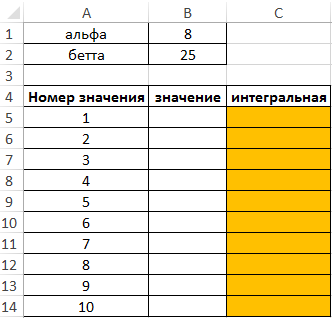
Для нахождения случайных чисел, имеющих распределение Вейбулла, используем обратную функцию:

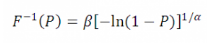
Вместо значения (1-P) будем вводить результат выполнения функции СЛЧИС, которая возвращает числа из диапазона (0;1), соответствующих допустимым значениям вероятности.

Для заполнения столбца «значение» используем формулу:

Ячейки в формуле «закреплены» с помощью “$” для получения корректных результатов при растягивании формулы:

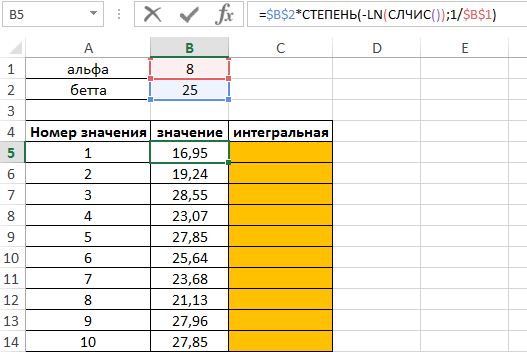
Поскольку при выполнении любого действия на листе функция СЛЧИС будет выполнять пересчет, выделим полученные числа и вставим в те же ячейки как значения (с помощью инструмента «Специальная вставка»).

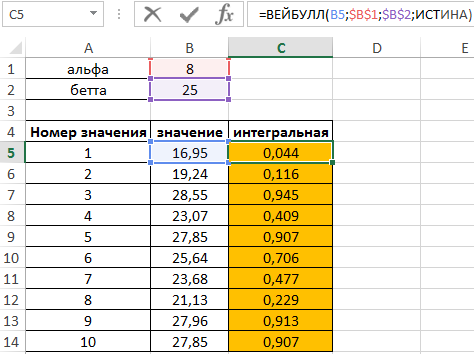
Для определения искомых значений выделим ячейки C5:C14 и запишем следующую формулу:

Результат вычислений:

Правила использования функции ВЕЙБУЛЛ в Excel

Функция имеет следующий синтаксис:

=ВЕЙБУЛЛ(x;альфа;бета;интегральная)

Описание аргументов (все являются обязательными):

• x – принимает числовое значение некоторой величины с распределением Вейбулла, для которой необходимо определить функцию;
• альфа – принимает числовое значение, характеризующее α-параметр распределения;
• бета – принимает числовое значение, которое характеризует β-параметр распределения;
• интегральная – принимает данные логического типа, определяющие форму вычисляемой функции: ИСТИНА – будет возвращена интегральная функция, ЛОЖЬ – будет возвращена функция плотности распределения Вейбулла.

Примечания:

1. Первые три аргумента функции должны принимать числовые значения или данные, которые могут быть преобразованы к числам, иначе результатом выполнения функции ВЕЙБУЛЛ будет код ошибки #ЗНАЧ!
2. Если аргумент x принимает значение 0, функция вернет 0 (нуль) при любых значениях остальных аргументов. Если первый аргумент (x) указан числом из диапазона отрицательных значений, будет возвращен код ошибки #ЧИСЛО! Аналогичная ошибка возникает, если аргументы, характеризующие α-параметр и β-параметр соответственно не взяты из диапазона положительных значений (0 также исключен).
3. Последний аргумент может указан в виде числа, соответствующего логическим значениям: 1 – ИСТИНА, 0 – ЛОЖЬ.