Решение транспортной задачи методом потенциалов в Excel с примером
Решим транспортную задачу методом потенциалов. Нам известны торговые запасы, потребительские запросы и стоимость доставки за единицу продукции. Сделаем три исходные таблицы.
Построим опорный план транспортной задачи с помощью инструмента «Поиск решений». Рядом составим такие же по объему таблицы с пустыми ячейками. Таблица А – аналог стоимостной, Б – «запасов», В – «спроса».
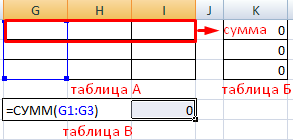
Элементы таблицы Б – сумма соответствующих строк в таблице А. Элементы таблицы В – сумма соответствующих столбцов в таблице А.
Отдельно составим результирующую таблицу Г. В ней отразятся оптимальные транспортные расходы. Каждый элемент таблицы Г – произведение элемента А и соответствующего элемента стоимостной таблицы.
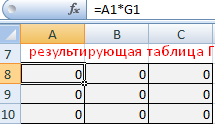
В отдельном месте листа введем формулу функции: =СУММПРОИЗВ(A1:C3;G1:I3)
Первый массив – стоимостная таблица, второй – диапазон А.
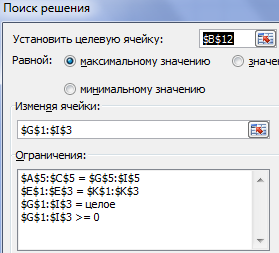
Ставим курсор в ячейку со значением функции. Вызываем инструмент «Поиск решения». Заполняем диалоговое окно:
- Целевая ячейка – ссылка на ячейку со значением функции.
- Она должна быть равна «максимальному значению», как наиболее выгодному для перевозчика.
- Команда изменяет значения ячеек в таблице А. Значения – целые числа.
- Диапазон таблицы Б = «Запасам».
- Диапазон В = «Потребительскому спросу».
В открытом диалоговом окне нажимаем кнопку «Параметры» и устанавливаем следующие настройки:
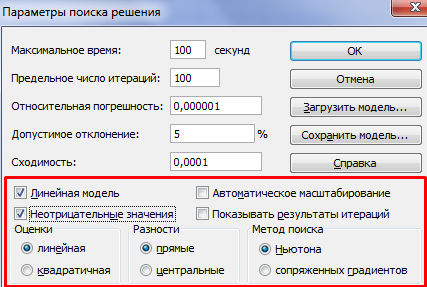
Жмем ОК – «Выполнить». Получаем опорный план транспортной задачи:
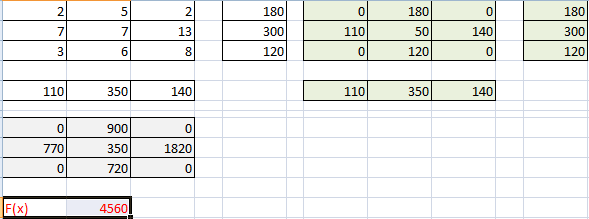
Он залит бледно-зеленым цветом. Ячейки со значениями выше нуля называются «базисными», «занятыми». Ячейки со значением 0 – «свободными».
Далее действуем по плану:
Посчитаем число занятых клеток с помощью функции СЧЕТЕСЛИ.
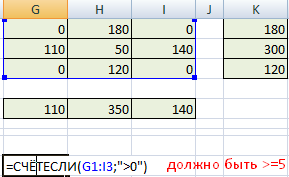
Так как результат равен 5, опорный план является не вырожденным. Проверим оптимальность опорного плана – найдем потенциалы по занятым клеткам.
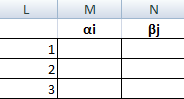
Нужно составить систему уравнений. Предполагается, что αj = 0, а αi + βj = сij (стоимость доставки единицы груза). Вызываем команду «Поиск решения». Вносим условия системы уравнений в качестве ограничений.
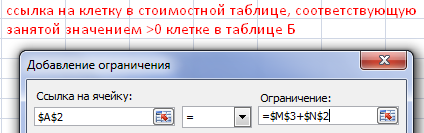
Заполненное диалоговое окно:
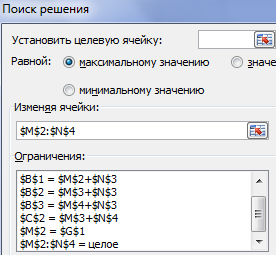
Результат работы инструмента «Поиск решения»:
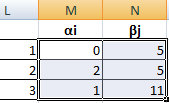
Посчитаем оценки свободных клеток. Формула: сij – (αi + βj). Берем свободную клетку из таблицы А. Смотрим ее значение в стоимостной таблице. Это будет сij. Далее смотрим, какие потенциалы соответствуют данной клетке. Вставляем их значения в формулу.
В программе Excel найдем оценки с помощью математических операторов и ссылок на соответствующие ячейки.
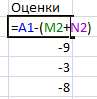
План считается оптимальным, если оценки больше или равны 0. В нашем случае получились отрицательные значения – план не является оптимальным. Поэтому двигаемся дальше.
Находим, какой клетке в таблице А соответствует минимальная оценка. Строим для этой клетки цикл – замкнутую ломаную линию. Условия: обязательно чередование вертикального и горизонтального направления, только по базисным клеткам.
В исходной клетке (с минимальной оценкой) ставим знак «+». Далее чередуем: «-», «+» и т.д.
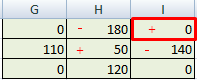
В таблице стоимости находим минимальное значение со знаком «-».
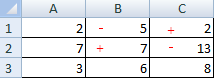
В нашем примере – это «5», ячейка В1. Эту клетку нужно убрать из базиса. А ячейку с минимальной оценкой сделать базисной.
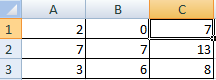
С учетом изменившихся данных вновь строим опорный план транспортной задачи. Применяем инструмент «Поиск решения». Пересчитанный план перевозок выглядит так:
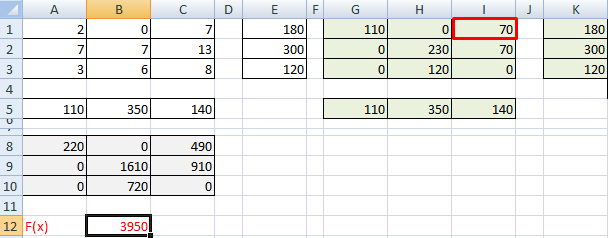
Обратите внимание: ячейка I1 (где была минимальная оценка) стала базисной, занятой.
Скачать пример решения транспортной задачи
Проводим те же расчеты для нового плана (с пункта №1): находим потенциалы, оценки свободных клеток для проверки оптимальности. И так до тех пор, пока оценки свободных клеток не будут больше или равны 0.