Функция РЯД.СУММ для расчета суммы степенных рядов в Excel

Функция РЯД.СУММ в Excel предназначена для расчета суммы степенного ряда типа a1xn+a2x(n+m)+a3x(n+2m)+…+aix(n+(i-1)m), где:

  • a – некоторый коэффициент;
  • x –переменная ряда;
  • n – показатель степени независимой переменной для первого члена ряда;
  • m – количественная характеристика изменения показателя степени независимой переменной.

Функция РЯД.СУММ производит расчет суммы членов степенного ряда на основе известных значений, переданных в качестве ее аргументов, и возвращает соответствующее числовое значение.

Примеры использования функции РЯД.СУММ в Excel

Пример 1. Рассчитать сумму первых пяти членов в ряду типа f(x)=∑i=0∞aix(n+(i-1)), если x имеет значение 5, начальная степень переменной n=1 и для каждого последующего члена увеличивается на 1, коэффициенты a приведены в таблице Excel.

Вид исходной таблицы:

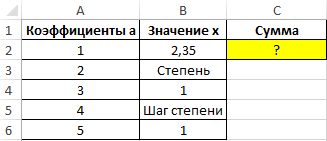
Пример 1.

Расчет производится по следующей формуле:

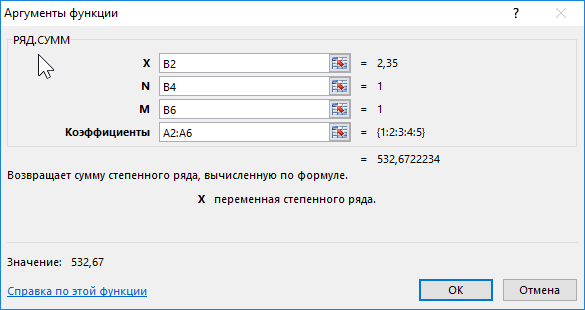
РЯД.СУММ.

Описание аргументов:

  • B2 – значение переменной x степенного ряда;
  • B4 - показатель степени переменной;
  • B6 – шаг увеличения степени переменной;
  • A2:A6 – диапазон ячеек, содержащих значения коэффициентов a.

Результат вычислений:

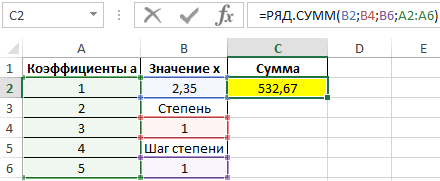
Рассчет суммы пяти членов в ряду.

Сумма степенного ряда составила 532,67.



Определение синуса методом разложения на ряд Маклорена в Excel

Пример 2. Определить значение sin1 с точностью до пяти знаков после запятой методом разложения функции sinx на ряд Маклорена.

Функция sinx может быть представлена в виде ряда:

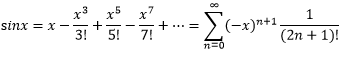
Пример 2.

Часть выражения 1/(2n+1)! является коэффициентом a степенного ряда.

Нулевым коэффициентом ряда является 1 (поскольку первое значение – x, который по условию равен 1) a для остальных используем формулу:

=1/ФАКТР(2*1+1)

Функция ФАКТР используется для определения факториала числа. Аналогично рассчитаем значения еще двух коэффициентов и введем остальные данные:

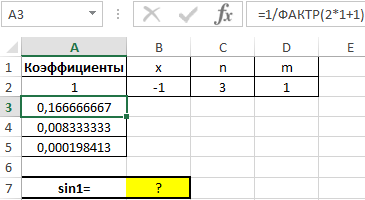
ФАКТР.

Для расчета используем формулу:

=ОКРУГЛ(A2+РЯД.СУММ(B2;C2;D2;A3:A5);5)

Описание аргументов:

  • A2 – нулевой коэффициент (вынесен за пределы формулы);
  • B2 – значение переменной;
  • C2 – показатель степени переменной первого члена последовательности;
  • A3:A5 – диапазон ячеек, содержащих значения коэффициентов.

Результат вычислений округляется функцией ОКРУГЛ до 5 знаков после запятой.

Результат вычислений:

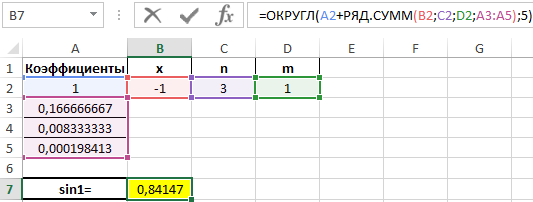
Определение синуса методом ряда Маклорена.

Расчет экспоненциального роста сложных процентов по функции РЯД.СУММ в Excel

Пример 3. В банк был сделан депозит под 15% годовых на некоторую сумму с непрерывным увеличением процентов на 5 лет. Определить показатель роста инвестиций с использованием разложения в степенной ряд.

Для расчета параметра роста можно использовать функцию y=ex. Как известно, ее можно разложить в ряд Маклорена следующим способом:

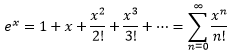
Пример 3.

Для расчета коэффициентов можно использовать формулу an=1/n!. Заполним таблицу исходных данных:

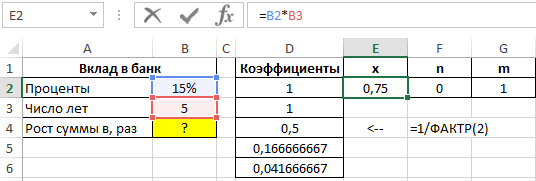
Заполним таблицу.

Значение x рассчитано как произведение ставки и времени действия договора. А расчета коэффициента такой же, как и в предыдущем примере: =1/ФАКТР(2), (3), (4)…

Предположим, данного количества коэффициентов достаточно для расчета. Используем следующую функцию:

=РЯД.СУММ(E2;F2;G2;D2:D6)

Полученное значение:

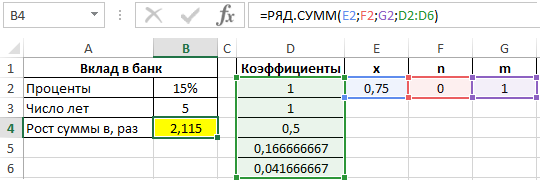
Расчет экспоненциального роста.

Проверим результат с использованием функции EXP:

EXP.

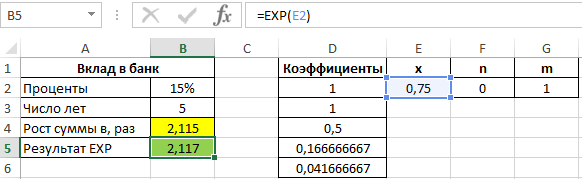
Рассчитаем погрешность по формуле:

=ABS(1-B5/B4)

Полученный результат:

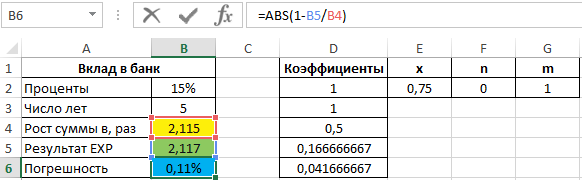
погрешность.

Начальная сумма вклада увеличится примерно в 2,12 раза. Значения членов степенного ряда, на который была разложена функция y=ex, убывают по мере роста показателя степени, демонстрируя, как по мере уменьшения временных интервалов снижается показатель роста. То есть, «старший» член ряда делает меньший «вклад» в общую сумму.

Особенности использования функции РЯД.СУММ в Excel

Функция имеет следующую синтаксическую запись:

=РЯД.СУММ(x; n; m;коэффициенты)

Описание аргументов (все являются обязательными для заполнения):

  • x – числовое значение, характеризующее переменную величину степенного ряда;
  • n – числовое значение, которое характеризует показатель степени переменной x для первого члена ряда;
  • m – числовое значение, характеризующее изменение показателя степени n переменной от первого члена ряда к последующим членам. Например, если m принимает значение 1, то для второго члена показатель степени равен n+(2-1)*1, третьего – n+(3-1)*1 (то есть, n+2), а для i-го члена показатель степени переменной рассчитывается как n+(i-1)*1;
  • коэффициенты – одно или несколько числовых значений, характеризующие значения коэффициентов a1, a2, a3,…,ai в выражении a1xn+a2x(n+m)+a3x(n+2m)+…+aix(n+(i-1)m).

Примечания 1:

  1. Любой аргумент рассматриваемой функции должен быть представлен данными числового типа, именем или текстовой строкой, преобразуемыми в число. Если один или несколько аргументов функции РЯД.СУММ принимают значения не преобразуемых к числовым значениям типов данных, результатом выполнения данной функции будет код ошибки #ЗНАЧ!.
  2. Функция не выполняет автоматического преобразования логических ИСТИНА и ЛОЖЬ к числовым данным 1 и 0 соответственно. Запись типа =РЯД.СУММ(ИСТИНА;1;1;1) вернет код ошибки #ЗНАЧ!.
  3. Аргумент коэффициенты может принимать одно или несколько значений в форме диапазона ячеек или массива данных (например, =РЯД.СУММ(1;2;1;A1:A8), или =РЯД.СУММ(1;1;1;{1;2;3;4;5}). Количество элементов массива, переданного в качестве аргумента коэффициенты, или число ячеек в переданной ссылке на диапазон регламентирует количество членов степенного ряда, сумму которых вычисляет рассматриваемая функция.
  4. Функция РЯД,СУММ не может быть использована в качестве формулы массива. Например, выражение типа =РЯД.СУММ(A1:A4;1;1;{1;2;3;4}) вернет диапазон из четырех ячеек с кодами ошибки #ЗНАЧ!.

Примечания 2:

  1. Степенным рядом является выражение типа f(x)=∑n=0∞=0anxn, где значения коэффициентов a принадлежат определенному диапазону величин (алгебраическому кольцу R).
  2. Одной из основных характеристик числового ряда является его сходимость (или расходимость). Сходимым рядом является последовательность, сумма членов которой является конечной величиной. Соответственно, если ряд расходится, это означает, что сумма бесконечного числа его членов является бесконечной величиной. Примером сходимого ряда может служить сумма членов бесконечно убывающей геометрической прогрессии.
  3. Для упрощенного представления (аппроксимации) существуют различные методы их разложения на степенные ряды. Нахождение суммы определенного количества членов такого ряда позволяет добиться довольно точного результата. При этом последующие члены представляют собой настолько малые величины, что ими можно пренебречь при расчете общей суммы членов.

en ru