Наиболее часто используемые формулы в Excel: процент и маржа

Примеры, описанные в этом уроке, доступны в файле Excel: Часто Используемые Формулы.xlsx, только их самостоятельное написание гарантирует, что вы запомните этот урок.

Самые популярные формулы в Excel: расчет процентов и маржи

Зачастую знание самого Excelя оказывается недостаточным и необходимо знание основных математических формул.

Много раз я уже убеждался, что даже человек с базовым экономическим образованием сталкивался с проблемой расчета цены без НДС имея такие данные: цена с НДС составляет 100$ и ставка НДС - 23%, и с удивлением утверждавшего, что он не в состоянии это сделать.

Ниже я представляю решение проблем, с которыми чаще всего сталкивается обычный сотрудник или кандидат на должность, где требуется знание Excel.



Формулы расчета процентов в Excel

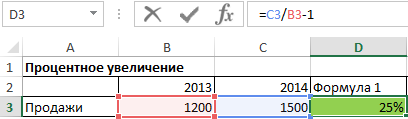
Процентное увеличение вычисляем по следующей формуле:

Увеличение процента = новая стоимость / старая стоимость - 1

Эта формула использовалась в следующем примере для расчета процентного увеличения, которое составило 25%.

Ту же формулу также можно написать в следующей форме:

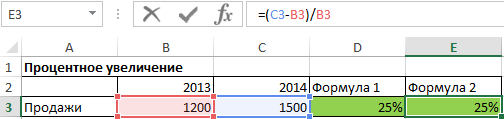
Прибавление процента = (новая стоимость – старая стоимость) / старая стоимость

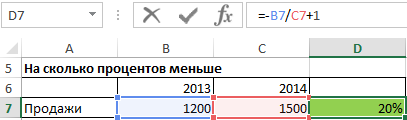
Иногда бывает, что процентное изменение за год рассчитывается «с другой стороны», в приведенном ниже примере мы можем сказать, что продажи в 2013 году были на 20% меньше, чем в 2014 году. Получатели такой информации недолго думая запоминают, что разница составляет 20%, тогда как на самом деле, как мы рассчитали в примере 1 (этот пример и предыдущий имеют одни и те же данные), она составляет 25%.

Это является преднамеренным введением в заблуждение получателя информации, и я не рекомендую использовать такой подход, разве что кто-то занимается политикой и должен придерживаться принятых в этой сфере стандартов.

Чтобы найти процентное отношение, например, какого-то товара в общем объеме продаж, мы делим объем продажи этого товара на общий объем продаж.

Процентное отношение = продажи товара A / общий объем продаж

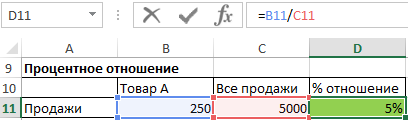
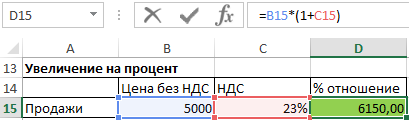
Для увеличения заданного значения на процент, например, для увеличения цены на 23% налога на добавленную стоимость, служит следующая формула:

Стоимость с НДС = стоимость без учета НДС * (1 + процент изменения)

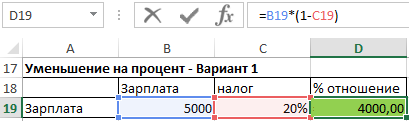
Аналогично выглядит формула уменьшения значения на процент, с той лишь разницей, что вместо знака плюс используется минус:

Новое значение = Старое значение * (1 - процент изменения)

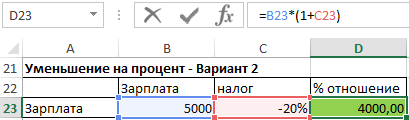
Иногда процент, на который нам нужно что-то уменьшить, дается со знаком минус (уменьшить на -20%), что теоретически является ошибкой (два минуса должны давать плюс), но, к сожалению, такой вариант популярен и должен пониматься как уменьшение на 20%. В таком случае используем ту же формулу, что и при увеличении на процент (минус уже в %).

Новое значение = Старое значение * (1 + проценты изменения)

И конечно же, уменьшить значение на процент - это одно, а "вывести" процент который был добавлен - совсем другое.

В следующем примере мы бы хотели бы найти цену без НДС от цены с НДС, НДС составляет 23 %.

Используем следующую формулу. Для того чтобы добавить определенный процент к значению, мы умножали значение на (1 + %), чтобы "вывести" процент - разделим значение на (1 + %) (деление является противоположным умножению действием).

Стоимость без НДС = Стоимость с НДС / (1 + % НДС)

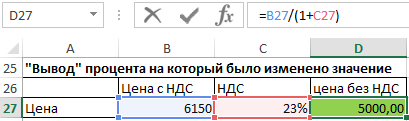
Как вы можете видеть, в приведенном примере нам удалось получить первоначальное значение цены без НДС, показанного на двух примерах выше.

Многие люди задают вопрос, почему обратным действием для увеличения значения на какой-то процент не является уменьшение на тот же процент.

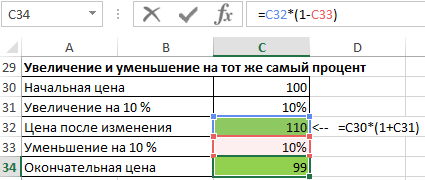
Давайте рассмотрим следующий пример, в котором цена была изменена дважды.

Начальная цена составляла 100$, она была увеличена на 10%, а после этого изменения она составляла 110$ (10% от 100 это 10, 10 + 100 = 110).

После первого изменения цена была снижена на 10% и в итоге составила 99$ (10% от 110 это 11). 110 -11 это 99).

Как видно, цена не вернулась к своему первоначальному значению. Чем больше было бы процентное изменение, тем больше была ба разница между начальной и окончательной ценой.

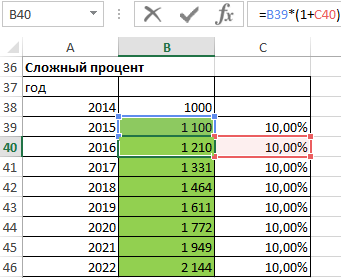
В приведенном ниже примере стоимость какой-то инвестиций увеличивается на 10% каждый год, мы хотели бы рассчитать, за сколько лет эта величина удвоится.

В первой из зеленых ячеек вводим формулу увеличения на процент и перетаскиваем ее в следующие ячейки. Удвоения этой суммы мы не должны ждать аж десять лет. Величина будет в два раза больше первоначальной суммы в седьмом году, а в восьмом значительно превысит свою двукратность. Происходит так, потому что процент во втором и каждом последующем инвестиционном году рассчитывается не из первоначальной суммы, а из уже увеличенной суммы.

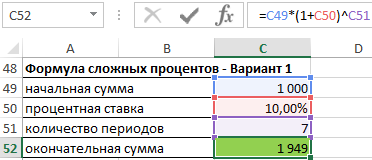
Тот же результат можно получить гораздо быстрее, используя формулу для сложных процентов.

Окончательная сумма = начальная сумма * (1 + процентная ставка) ^ количество периодов

символ ^ означает степень)

В следующем примере сложных процентов некто задается вопросом, если бы он положил на вклад 1 000 $ под фиксированную процентную ставку в размере 5 % годовых и с ежегодной капитализацией процентов, были бы его пра-пра-праправнуки через 200 лет миллионерами.

После применения вышеприведенной формулы к таким данным, на вышеупомянутый вопрос мы получим утвердительный ответ. Через 200 лет на счету будет сумма более 17 миллионов $.

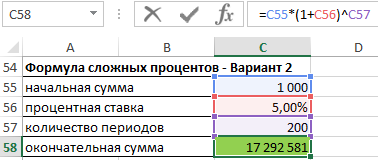
Если мы решим рассчитать ту же задачу с использованием 200 формул для увеличения на процент, отметим, что прирост суммы депозита на заключительном этапе несравненно больше, чем в начальные периоды. За последние несколько лет величина депозита увеличивалась почти на 1 млн. $ ежегодно.

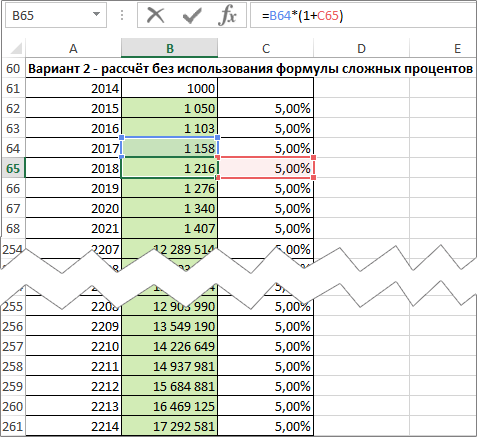
Такой рост величины депозита в последующие периоды типичен для экспоненциальных функций, то есть тех, в которых переменная, в данном случае количество лет, находится в степени.

Должны ли мы теперь поспешить в банки с целью открытия таких депозитных счетов? Если бы мы хотели рассмотреть эти расчеты не как пример, а серьезно, следовало бы нам также учесть инфляцию, риск банкротства банка, риск девальвации валюты депозита или даже смену системы, национализацию банковских депозитов, дефолт государства или войну. С учетом этих факторов, более разумным способом инвестирования 1 000 $, по-видимому, является использование их для повышения своей профессиональной квалификации, например, обучение Excel и VBA :-).

Читайте также: Прибавить и отнять процент в Excel от числа с примерами.

Формулы расчета маржи в Excel

Вычисление маржи для многих людей является большой проблемой, потому что они думают о добавлении маржи как о добавлении процента к заданной величине.

Фактически, маржа — это не процент от «накладных расходов», а процент, которым является прибыль в конечной цене продукта или услуги.

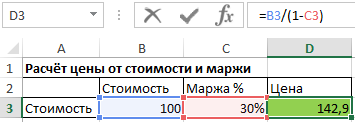
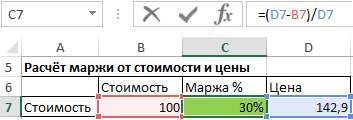
При данной стоимости и проценте маржи, цена рассчитывается по следующей формуле:

Цена = Стоимость / (1- процент маржи)

Маржа должна быть менее 100%, потому что невозможно продать что-то, зарабатывая при этом 100% и более, при этом каждая хозяйственная деятельность связана с некоторыми издержками.

В то же время, маржа может быть отрицательной, тогда компания продает свои товары или услуги ниже себестоимости и теряет на каждой операции.

Вопреки тому как может казаться, это не редкое явление, в некоторых отраслях, например, при продаже принтеров нормальным явлениям является их продажа ниже себестоимости. Производители покрывают эти потери продавая услуги и картриджи (чернила) с высокой маржей. Такая стратегия используется для упрощения привлечения клиентов.

Чтобы рассчитать маржу, зная стоимость и цену, используем следующую формулу:

Процент маржи = (цена – стоимость) / цена

Вышеуказанная формула также может быть записана как: процент маржи = 1 - стоимость / цена.

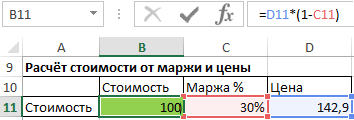
Однако, если искомым элементом является стоимость, мы используем следующую формулу, такую же, которую мы используем для уменьшения суммы на процент.

Другими словами, мы понижаем цену на размер маржи и получаем стоимость.

Стоимость = цена * (1 - маржа)

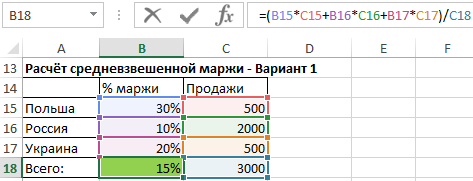
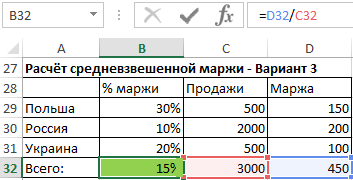
Средневзвешенная маржа от продаж

Для вычисления средней маржи мы не можем использовать обычное среднее значение, мы должны вычислить его с использованием средневзвешенного значения, где весом являются объёмы продаж.

Мы можем сделать это тремя способами:

1. Используя первый способ, мы перемножаем каждую процентную маржу на соответствующий ей объем продаж, суммируем результаты и эту сумму делим на сумму всего объёма продаж. Эта формула даёт нам полный контроль над методом расчёта и позволяет понять, на чём основывается средневзвешенное значение.

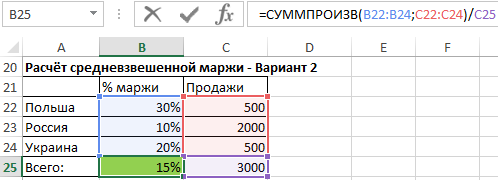
2. При использовании второго способа, нам служит функция СУММПРОИЗВ, которая суммирует произведения маржи и соответствующий ей объем продаж. Результат, который возвращает функция мы должны ещё разделить на общий объём продаж. Эта функция подробно описана в статье «Основные функции».

3. Третий способ является для многих самым простым, но требуется создание дополнительного столбца с маржей от суммы каждой продажи. Значения в столбце K получаем путём умножения каждой процентной маржи на соответствующий ей объем продаж. Чтобы рассчитать средневзвешенную маржу, просто разделите сумму маржи на сумму всех продаж.

Читайте также: Как посчитать маржу и наценку в Excel.

Я предлагаю вам удалить содержимое всех зелёных полей в файле упражнений к этому уроку и самостоятельно ввести формулы без подглядывания в вышеприведённое описание. Если вам удастся ввести их все правильно, значит вы освоили этот материал, если нет - всегда можно начать снова и снова, и так пока не получите результат.