Коэффициент парной корреляции в Excel
Коэффициент корреляции отражает степень взаимосвязи между двумя показателями. Всегда принимает значение от -1 до 1. Если коэффициент расположился около 0, то говорят об отсутствии связи между переменными.
Если значение близко к единице (от 0,9, например), то между наблюдаемыми объектами существует сильная прямая взаимосвязь. Если коэффициент близок к другой крайней точке диапазона (-1), то между переменными имеется сильная обратная взаимосвязь. Когда значение находится где-то посередине от 0 до 1 или от 0 до -1, то речь идет о слабой связи (прямой или обратной). Такую взаимосвязь обычно не учитывают: считается, что ее нет.
Расчет коэффициента корреляции в Excel
Рассмотрим на примере способы расчета коэффициента корреляции, особенности прямой и обратной взаимосвязи между переменными.
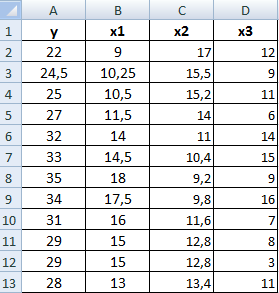
Значения показателей x и y:
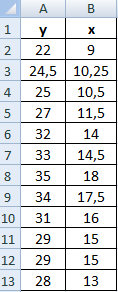
Y – независимая переменная, x – зависимая. Необходимо найти силу (сильная / слабая) и направление (прямая / обратная) связи между ними. Формула коэффициента корреляции выглядит так:
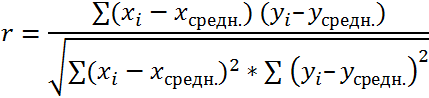
Чтобы упростить ее понимание, разобьем на несколько несложных элементов.
- Найдем средние значения переменных, используя функцию СРЗНАЧ:
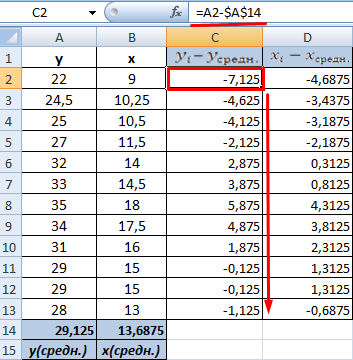
- Посчитаем разницу каждого y и yсредн., каждого х и хсредн. Используем математический оператор «-».
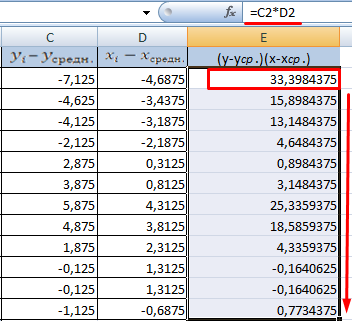
- Теперь перемножим найденные разности:
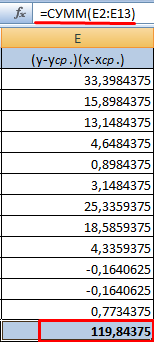
- Найдем сумму значений в данной колонке. Это и будет числитель.
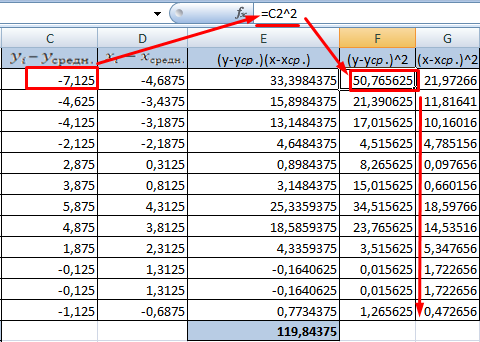
- Для расчета знаменателя разницы y и y-средн., х и х-средн. Нужно возвести в квадрат.
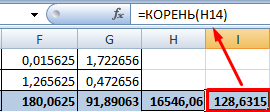
- Находим суммы значений в полученных колонках (с помощью функции АВТОСУММА). Перемножаем их. Результат возводим в квадрат (функция КОРЕНЬ).
- Осталось посчитать частное (числитель и знаменатель уже известны).
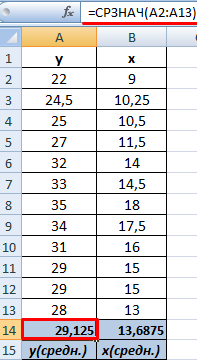
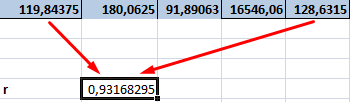
Между переменными определяется сильная прямая связь.
Встроенная функция КОРРЕЛ позволяет избежать сложных расчетов. Рассчитаем коэффициент парной корреляции в Excel с ее помощью. Вызываем мастер функций. Находим нужную. Аргументы функции – массив значений y и массив значений х:
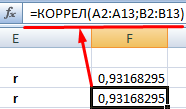
Покажем значения переменных на графике:
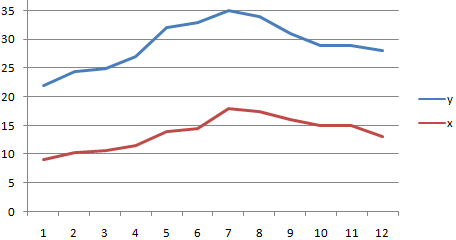
Видна сильная связь между y и х, т.к. линии идут практически параллельно друг другу. Взаимосвязь прямая: растет y – растет х, уменьшается y – уменьшается х.
Матрица парных коэффициентов корреляции в Excel
Корреляционная матрица представляет собой таблицу, на пересечении строк и столбцов которой находятся коэффициенты корреляции между соответствующими значениями. Имеет смысл ее строить для нескольких переменных.
Матрица коэффициентов корреляции в Excel строится с помощью инструмента «Корреляция» из пакета «Анализ данных».
- На вкладке «Данные» в группе «Анализ» открываем пакет «Анализ данных» (для версии 2007). Если кнопка недоступна, нужно ее добавить («Параметры Excel» - «Надстройки»). В списке инструментов анализа выбираем «Корреляция».
- Нажимаем ОК. Задаем параметры для анализа данных. Входной интервал – диапазон ячеек со значениями. Группирование – по столбцам (анализируемые данные сгруппированы в столбцы). Выходной интервал – ссылка на ячейку, с которой начнется построение матрицы. Размер диапазона определится автоматически.
- После нажатия ОК в выходном диапазоне появляется корреляционная матрица. На пересечении строк и столбцов – коэффициенты корреляции. Если координаты совпадают, то выводится значение 1.
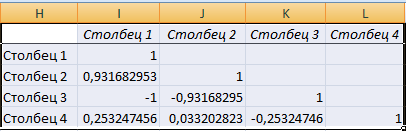
Между значениями y и х1 обнаружена сильная прямая взаимосвязь. Между х1 и х2 имеется сильная обратная связь. Связь со значениями в столбце х3 практически отсутствует.
Изобразим наглядно корреляционные отношения с помощью графиков.
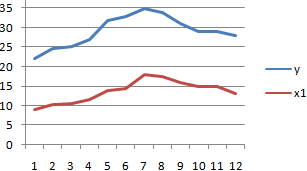
- Сильная прямая связь между y и х1.
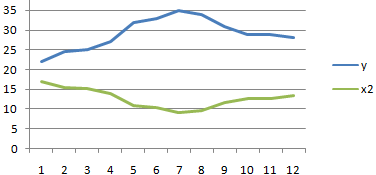
- Сильная обратная связь между y и х2. Изменения значений происходят параллельно друг другу. Но если y растет, х падает. Значения y увеличиваются – значения х уменьшаются.
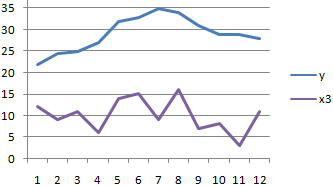
- Отсутствие взаимосвязи между значениями y и х3. Изменения х3 происходят хаотично и никак не соотносятся с изменениями y.
Скачать вычисление коэффициента парной корреляции в Excel
Для чего нужен такой коэффициент? Для определения взаимосвязи между наблюдаемыми явлениями и составления прогнозов.