Решение транспортной задачи в Excel с примером и описанием

Практически все транспортные задачи имеют единую математическую модель. Классический вариант решения иллюстрирует самый экономный план перевозок одинаковых или схожих продуктов от производственного объекта в пункт потребления.

Планирование перевозок с помощью математических и вычислительных методов дает хороший экономический эффект.

Виды транспортных задач

Условия и ограничения транспортной задачи достаточно обширны и разнообразны. Поэтому для ее решения разработаны специальные методы. С помощью любого из них можно найти опорное решение. А впоследствии улучшить его и получить оптимальный вариант.

Условия транспортной задачи можно представить двумя способами:

в виде схемы;
в виде матрицы.

В процессе решения могут быть ограничения (либо задача решается без них).

По характеру условий различают следующие типы транспортных задач:

открытые открытые транспортные задачи (запас товара у поставщика не совпадает с потребностью в товаре у потребителя);
закрытые (суммарные запасы продукции у поставщиков и потребителей совпадают).

Закрытая транспортная задача может решаться методом потенциалов. Она всегда разрешима. Открытый тип сводят к закрытому с помощью прибавления к суммарному запасу или потребности в товаре недостающих единиц, чтобы добиться равенства.

Пример решения транспортной задачи в Excel

Предприятия А1, А2, А3 и А4 производят однородную продукцию а1, а2, а3 и а4, соответственно. В условных единицах – 246, 186, 196 и 197. Затем товар поступает в пять пунктов назначения: В1, В2, В3, В4 и В5. Это потребители продукции. Они готовы ежедневно принимать 136, 171, 71, 261 и 186 единиц товара.

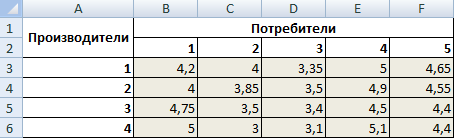
Стоимость перевозки единицы продукции с учетом удаленности от пункта назначения:

Производители	Потребители					Объем производства
	В1	В2	В3	В4	В5
А1	4,2	4	3,35	5	4,65	246
А2	4	3,85	3,5	4,9	4,55	186
А3	4,75	3,5	3,4	4,5	4,4	196
А4	5	3	3,1	5,1	4,4	197
Объем потребления	136	171	71	261	186

Задача: минимизировать транспортные расходы по перевозке продукции.

Проверим, является ли модель транспортной задачи сбалансированной. Для этого все количество производимого товара сравним с суммарным объемом потребности в продукции: 246 + 186 + 196 + 197 = 136 + 171 + 71 + 261 + 186. Вывод – модель сбалансированная.
Сформулируем ограничения: объем перевозимой продукции не может быть отрицательным и весь товар должен быть доставлен к пунктам назначения (т.к. модель сбалансированная).
Введем стоимость перевозки единицы продукции в рабочие ячейки Excel.

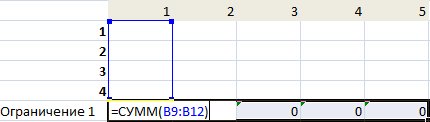
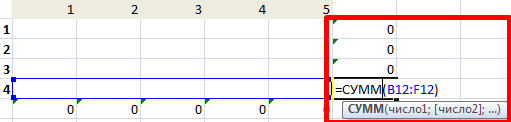
Введем формулы для расчета суммарной потребности в товаре. Это будет первое ограничение.

Введем формулы для расчета суммарного объема производства. Это будет второе ограничение.

Вносим известные значения потребности в товаре и объема производства.

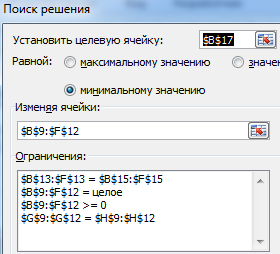
Вводим формулу целевой функции СУММПРОИЗВ(B3:F6; B9:F12), где первый массив (B3:F6) – стоимость единицы перевозки товаров. Второй (B9:F12) – искомые значения транспортных расходов.
Вызываем команду «Поиск решения» на закладке «Данные» (если там нет данного инструмента, то его нужно подключить в настройках Excel, а как это сделать описано в статье: расширенные возможности финансового анализа). Заполняем диалоговое окно. В графе «Установить целевую ячейку» - ссылка на целевую функцию. Ставим галочку «Равной минимальному значению». В поле «Изменяя ячейки» - массив искомых критериев. В поле «Ограничения»: искомый массив >=0, целые числа; «ограничение 1» = объему потребностей; «ограничение 2» = объему производства.

Нажимаем «Выполнить». Команда подберет оптимальные переменные при заданных ограничениях.

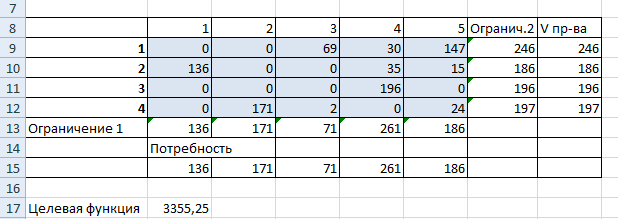
Так выглядит «сырой» вариант работы инструмента. Экспериментируя с полученными данными, находим подходящие значения.

Решение открытой транспортной задачи в Excel

При таком типе возможны два варианта развития событий:

суммарный объем производства превышает суммарную потребность в товаре;
суммарная потребность больше суммы запасов.

Открытую транспортную задачу приводят к закрытому типу. В первом случае вводят фиктивного потребителя. Его потребности равны разнице всего объема производства и суммы существующих потребностей.

Во втором случае вводят фиктивного поставщика. Объем его производства равен разнице суммарной потребности и суммарных запасов.

Единица перевозки груза для фиктивного участника равняется 0.

Когда все преобразования выполнены, транспортная задача становится закрытой и решается обычным способом.